問題[速さの問題]
|
|
|
|
|
|
甲地から乙地までの高速バスがあって、A社とB社の2台のバスが走っています。 ある日路線内で渋滞があって、この区間を2社のバスは同じ速さで徐行運転しました。 |
|
|
|
|
|
解答例1[徐行区間だけで考える]
| なにわさん、ミト清さん、HAJIさん、Taroさん、 龍さん、Nなヒトさん、かず。さん、もありすさん、kasamaさん、 まるケンさん、tomhさん、スモークマンさん、他 |
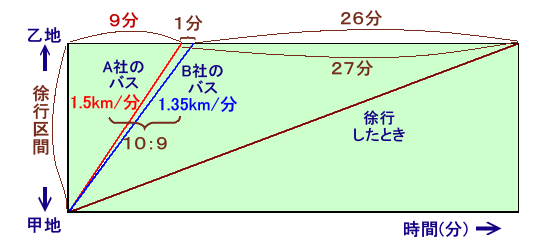
徐行区間だけについて下記のようなダイアグラムで考えます。
通常時のA社、B社のバス、および徐行した場合を、それぞれ便宜上同じ時間に徐行区間に入ったものとします。
通常時におけるバスの速度比は、90km/h:81km/h=1.5km/分:1.35km/分=10:9より、
所要時間の比は、9:10となります。ところが、予定よりA社のバスは27分、B社は26分遅れたことから、
通常時における徐行区間の所要時間は、B社のバスがA社よりも1分多いことになります。従って、A社の所要時間=9分、B社の所要時間=10分と分かります。
よって、B社のバスの場合で考えると、
徐行区間の長さ=1.35km/分×10分=13.5km
と求まります。答 13.5km
以上
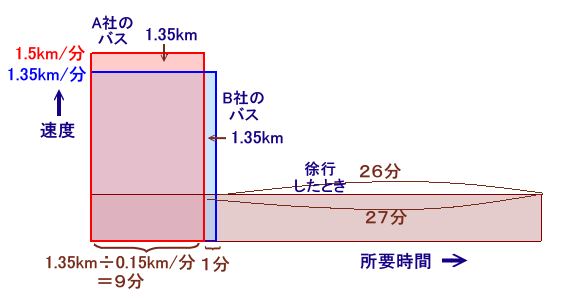
(別解)縦に速度、横に所要時間、面積が走行距離(速度×所要時間)となる面積図で考えます。
A社バスの走行距離とB社バスの走行距離を表す長方形の面積は等しいので、
はみ出た部分の長方形の面積も等しくなります。
B社バスで計算すると、これらは1.35km/分×(27−26)分=1.35kmとなります。従って、
A社バスの所要時間=1.35km÷(1.5−1.35)km/分=9分
B社バスの所要時間=9分+1分=10分
となります。以下、同様。