問題[空間図形(場合の数)]
|
|
|
|
|
|
|
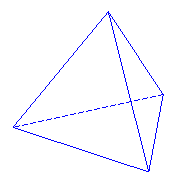 |
左図のような、4つの同じ正三角形でつくられた三角錐を、正四面体といいます。 |
|
|
|
|
|
|
解答例1[底面を1色固定 、絶対合格するぞ〜、固定して回転、上から見て三分割、展開図を描く、二面を固定]
| みかんさん、いおくらだいすけさん、AYAKAさん、智乃介さん、ゆうしゃさん、 Taroさん、長野 美光さん、Nなヒトさん、tekiさん、 浜直君さん、ちこりんさん、パァ〜子さん、パリンさん、kasamaさん、 tomhさん、ピーターラビットさん、 ライスさん、ミト清さん、もありすさん、 ゴンともさん、 吉田貴法さん、 うんこさん、HAJIさん、 まるケンさん、坂内はむのすけさん、他 |
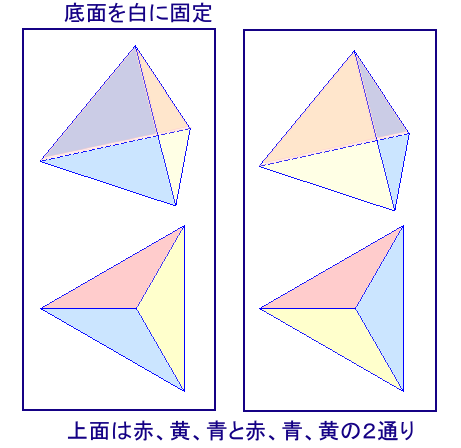
底面を1色固定(白色にします)して考えてみましょう。
残りの3面は、
円順列で考えると ・・・ (3−1)!=2×1=2通り
もう1色を固定(赤)すると ・・・ 赤の右に黄がくるか青がくるかの2通り
答 2通り
以上