問題[時計算]
|
|
|
|
|
|
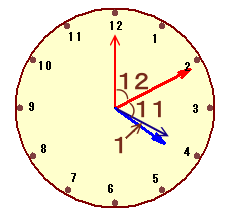
時計がちょうど4時を指しています。 |
|
|
|
|
|
解答例1[長針=12度/分、 短針の12時からの角度を半分にする、鶴亀算、絵を描いて比で解く]
| きょろ文さん、HAJIさん、なかじ達人さん、ぺんこさん、優太ぱぱさん、 Taroさん、ゴンともさん、 うんこさん、 ミックケリーさん、他 |
長針の速さは、短針の速さの12倍です。
従って、2等分になるまでの時間に短針の動いた角度を1とすると、長針の動いた角度は12となります。12時の方向と短針の方向の間の角度は、長針の動いた角度の2倍だから24、
従って、これから短針の動いた角度を差し引いた23が、12時から4時の間の20分に相当します。よって、この間に短針が動いた時間は、
20×12/23=240/23分
と求まります。答 240/23分
以上
[アニメON]を押すとアニメを表示します。
(その他の解法)
- 方程式を用いて解く ・・・ kuri,パリンさん、長野 美光さん、龍さん、mhayashiさん、 かず。さん、elmotitiさん、ゆうしゃさん、kasamaさん、パァ〜子さん、 tomhさん、みかんさん、坂内はむのすけさん、森よしさん、信三さん、他
長針は1時間=60分間に360度進むので、毎分360÷60=6度進みます。
一方、短針は12時間で360度進むので、毎分360÷60÷12=1/2度進みます。
従って、t分では、
t×6=(20×6+t×1/2)×1/2
これを解くと、t=240/23を得ます。: