問題[推理]
|
|
|
|
|
|
ゼッケン1番から6番までの6人が、5日間の日程で総当たり戦を行ないます。 ゼッケン1番の人は、初日から5日目までに「2番の人→3番の人→4番の人→5番の人→6番の人」の順に対戦しました。また、ゼッケン6番の人の初日の対戦相手は5番、2日目は4番の人でした。 では、ゼッケン2番の人は、初日から5日目までどのような順番で対戦しましたか? |
|
|
|
|
|
解答例1[表に整理する、 図を書いて求める、6番の人の3日目の対戦相手]
| 芝野享平さん、そうたさん、なかじ達人さん、りかさん、あさみさん、 HAJIさん、土橋 雅樹さん、鳳 奥人さん、かず。さん、パァ〜子さん、 elmotitiさん、tomhさん、kasamaさん、高木数学校さん、ののみさん、 アラちゃんさん、坂内はむのすけさん、tekiさん、こういちさん、トシえもんさん、 ともこさん、あすさん、ミト清さん、パリンさん、elmoさん、 晋弥さん、わかピョンさん、藤井健洋さん、じゅうたん島さん、ゴンともさん、あまれっとさん、Yyukomamaさん、あかねさん、スモークマンさん、冨田大輔さん、晋弥さん、tisaさん、みかんさん、mitchy_mathさん、 みかんさん、他 多数 |
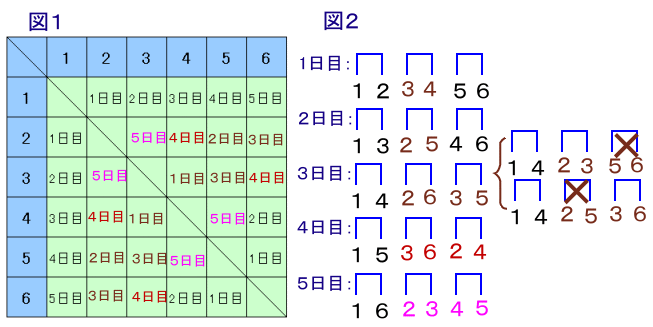
図1は各選手同士が何日目に対戦したかを表したもの、図2は各日毎にどの選手同士が対戦したかを表したものです。
1日目は、1番と2番、5番と6番の対戦が決まっていますから、残る1試合は3番と4番の対戦になります。(図2)
2日目も、1番と3番、4番と6番の対戦が決まっていますから、残る1試合は2番と5番の対戦になります。(図2)
3日目は、1番と4番の対戦だけ決まっています。(図2)
2番の対戦相手として3番、5番、6番の3ケースが考えられます。
2番対3番のとき ・・・ 残る1試合が5番対6番になりますが、この対戦は既に1日目に終わっているので不適
2番対5番のとき ・・・ この対戦は既に2日目に終わっているので不適
2番対6番のとき ・・・ 残る1試合が3番対5番になります..適
これらの結果を図1に反映すると、
5番の人の対戦が残っているのは、4番の人と5日目に行う試合のみです。
従って、図2から5日目の残る1試合は、2番と3番の対戦になります。また、6番の人の対戦が残っているのは、3番の人と4日目に行う試合のみです。
従って、図2から4日目の残る1試合は、2番と4番の対戦になります。以上で全ての対戦相手が決まりました。
2番の人の対戦相手は、1日目から順に
1番、5番、6番、4番、3番
となります。答 1番、5番、6番、4番、3番
以上