問題[規則性]
|
|
|
|
|
|
1から100までの整数を書いた100枚のカードを、裏向きにして順に円く
並べます。 このとき表向いているカードの中に、3の倍数は何 枚ありますか? |
|
|
|
|
|
解答例1[書いて数える、 紙に計算する、指折り数えた]
| ふうきさん、Taroさん、HAJIさん、ぺんこさん、わかピョンさん、 パリンさん、長野 美光さん、C-Dさん、みかんさん、ともこさん、 晋弥さん、ショウさん、浜直君さん、吉田佳薫さん、 kasamaさん、坂内はむのすけさん、☆まなえ☆さん、tomhさん、りかさん、 ppppさん、大岡 敏幸さん、こういちさん、ちいさん&かえるクンさん、空さん、 いさん、ochamuさん、kobaさん、 まーちゃんさん、そうたさん、他多数 |
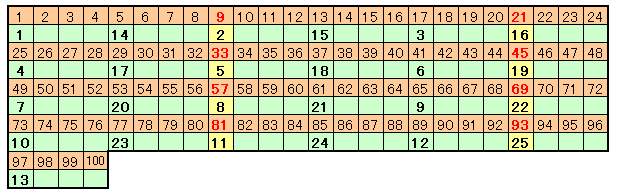
下記のように1から100までの整数を表にして考えます。
表向きにしていく順に番号を付けていくと、3巡目に入るところで元の1に戻り、
合計25枚のカードが表向きになりました。このうち、3の倍数は9、21、33、45、57、69、81、93の8枚です。
答 8枚
以上
(参考)式で考える
8と100の最小公倍数は200なので、200÷8=25枚のカードが表向きになります。
n枚目に表向きにするカードに書かれた整数をKnとします。
n=1〜13のとき、Kn=8(n−1)+1=9(n−1)−(n−2)
Knが3の倍数 → (n−2)が3の倍数
→ n=2、5、8、11の4個
n=14〜25のとき、Kn=8(n-14)+5=9(n−1)−(n−16)+3
Knが3の倍数 → (n−16)が3の倍数
→ n=16、19、22、25の4個となり、3の倍数は合計8枚となります。
(その他の解法)
- 卓上電卓を押す ・・・ ゴンともさん、さび^^さん、 他
- 計算機プログラム ・・・ ハラギャーテイさん、金閣と銀閣さん、 他