問題[平面図形]
|
|
|
|
|
|
|
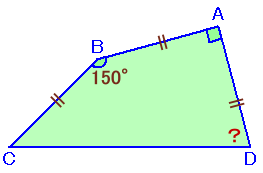 |
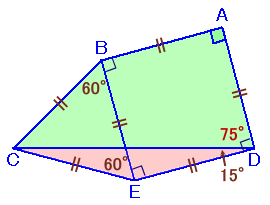
左図のような四角形ABCDがあって、AB=BC=AD、∠A=
90°、∠B=150°になっています。 |
|
|
|
|
|
|
解答例1[正方形と正三角形の性質の利用 、150度のところから半分に切り三角形2つ]
| たけのこさん、佐藤 広宣さん、りかさん、ゴンともさん、松本 律さん、 なかじ達人さん、大岡 敏幸さん、長野 美光さん、ミト清さん、tomhさん、 kasamaさん、スモークマンさん、ANGELさん、きょろ文さん、石田晃貴さん、 かんけりさん、 ちいさん&かえるクンさん、踊る大捜査線さん、他 |
四角形ABEDが正方形となるように点Eをとります。
すると、BE=AB=BCで∠CBE=150−90=60度、
よって、△BCEは正三角形となります。従って、CE=BC=ED、
よって、△ECDは二等辺三角形。∠CED=60+90=150度、
よって、∠CDE=(180−150)÷2=15度、
従って、∠ADC=90−15=75度と求まります。答 75度
以上
解答例2[対角線を引いて・・・]
| スマイルさん、はくさん、ピーターラビットさん、他 |
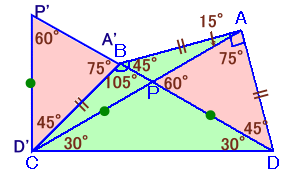
対角線ACとBDの交点をPとします。
BA=BCより△BCAは二等辺三角形で、∠ABC=150度より、
∠BAC=(180−150)÷2=15度。AB=AD、∠BAD=90度より、△ABDは直角二等辺三角形、
よって、∠ABD=∠ADB=45度。∠PAD=90−15=75度、∠APD=45+15=60度。
さて、△APDをADがBCと重なるように移動したものを△BP'Cとします。
すると、∠P'BC+∠CBD=75+105=180度より、
P、B、P'は一直線上に並びます。∠CP'P=∠CPP'=60度より、△CP'Pは二等辺三角形。
よって、DP=CP'=CP、
従って、△PCDは二等辺三角形となります。よって、∠PDC=∠APD÷2=60÷2=30度、
従って、∠ADC=45+30=75度と求まります。
解答例3[三角形ACDは二等辺三角形]
| まるケンさん、パリンさん、他 |
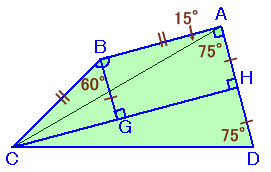
CからADに下ろした垂線の足をHとし、
BからCHに下ろした垂線の足をGとします。
∠CBG=150−90=60度より、
BG=BC×1/2となります。AD=BC、AH=BGより、AH=HD、
よって、△ACDは二等辺三角形となります。よって、∠ADC=∠CAD=90−15=75度と求まります。
解答例4[四角形=菱形+正三角形+二等辺三角形]
| mhayashiさん、他 |
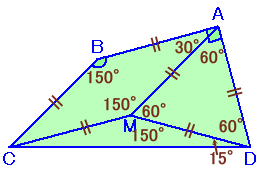
Cを通りABに平行な直線と、Aを通りBCと平行な直線の交点をMとします。
四角形ABCMは平行四辺形でAB=BCより、菱形になります。
よって、
AM=MC=AB=AD、
∠AMC=∠ABC=150度、
∠BAM=∠MCB=(360−150×2)÷2=30度
となります。すると、AM=ADで∠MAD=90−30=60度より、△AMDは正三角形となります。
よって、MD=AM=MCより、△MCDは二等辺三角形、
∠CMD=360−150−60=150度、
従って、∠MDC=(180−150)÷2=15度。よって、∠ADC=60+15=75度と求まります。