第１１０問の解答

問題［規則性]

問題図

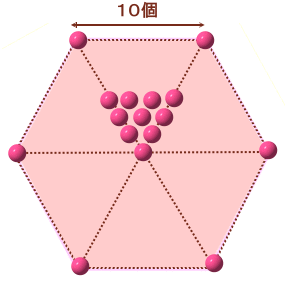左図のように、丸い石を１辺が１０個の正六角形の形に敷き詰めると、
石は全部で何個になりますか。

解答例１[45*6+1、45×5＋55＋1、36×6＋9×6＋1]

佐藤 仁信さん、mhayashiさん、鳳　奥人さん、ちこりんさん、踊る大捜査線さん、 さやかさん、なかじ達人さん、tekiさん、まちゃぴさん、まるケンさん、 智乃介さん、bunさん、浜直君さん、かず。さん、多佳子さん、大岡　敏幸さん、ほげさん、そうたさん、AYAKAさん、 mitchy_mathさん、高砂さん、ふじさきたつみさん、長野　美光さん、きょろ文さん、 mikiさん、りかさん、 　たけのこさん、清豚さん、デールさん、ともこさん、　Taroさん、パリンさん、kasamaさん、tomhさん、他

参考図１

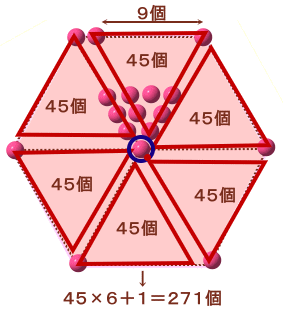
図のように、真ん中の１個を除いて６分割すると、
　１＋２＋・・・＋９＝４５個
ずつになります。

従って、全体では、
　４５×６＋１＝２７１個
と求まります。

答　 ２７１個

以上

解答例２[等差数列の和の公式、等差数列となんかの組み合わせ、中心から広げていく]

ゴンともさん、ゆうしゃさん、HAJIさん、スマイルさん、ユーサイさん、 他

参考図２

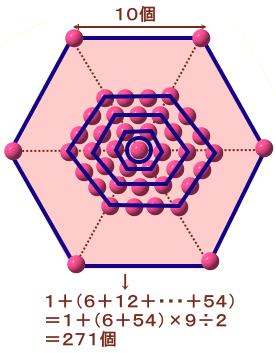
中心から２列目以降の個数を数えると、

  • ２列目　・・・　６個

  • ３列目　・・・　６×２＝１２個

  • ４列目　・・・　６個×３＝１８個
    ・・・

  • １０列目　・・・　６個×９＝５４個

と等差数列になります。

従って、
　合計＝１＋６×（１＋２＋３＋・・・＋９）
　　　　＝１＋６×４５
　　　　＝２７１個
と求まります。

解答例３[55×6−(9×6＋5)、愚直に]

ぺんこさん、スモークマンさん、他

参考図３

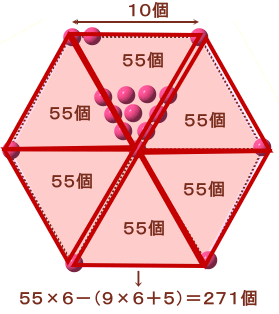
６分割した三角形部分の個数を数えると、
　１＋２＋３＋・・・＋１０＝５５個
になります。

ただしこの数え方は、正六角形の対角線部分のうち、
　中心部分以外の９個：２回ずつ
　中心部分：６回
数えています。

従って、
　　求める個数
　＝５５×６−（９×６＋５）
　＝２７１個
と求まります。

（その他の解法）