問題[空間図形]
|
|
|
|
|
|
|
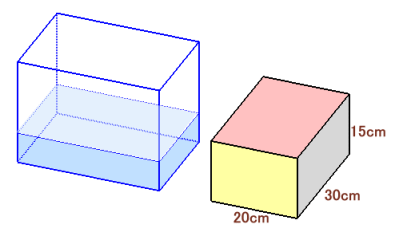 |
水の入った水槽と、15cm×20cm×30cmの直方体の重りがあります。
この重りを「15cm×20cmの面」を下にして水に沈めると、水深が12cmになります。 では、「20cm×30cmの面」を下にして水に沈めると、水深は何cmになりますか。 |
|
|
|
|
|
|
解答例1
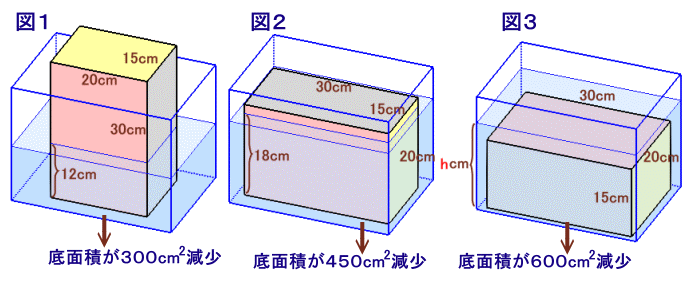
重りを「15cm×20cmの面」を下にして水に 沈めたとき(図1):
水がある部分の底面積は、元の水槽の底面積より15×20=300cm2減少します。重りを「15cm×30cmの面」を下にして水に 沈めたとき(図2):
水がある部分の底面積は、元の水槽の底面積より15×30=450cm2減少します。従って、これらの差は450−300=150cm2になります。
また、水深の比が12:18=2:3なので、底面積の比は3:2となります。
差が、150cm2なので、底面積はそれぞれ450cm2と300cm2。よって、
元の水槽の底面積は450+300=750cm2、
水の容積=450×12=5400cm3
と分かります。さて、重りを「20cm×30cmの面」を下にして水に 沈めたとき(図3):
水がある部分の底面積は、元の水槽の底面積より20×30=600cm2減少し、
750−600=150cm2になります。図3では、図2より底面積がさらに減少しているので、水深は図2の18cmより高くなります。
従って、重りの高さ15cmよりも高くなるので、重り全体が水の中にすっぽり沈むことになります。よって、
水深=(水の容積+重りの体積)÷水槽の底面積
=(5400+15×20×30)÷750
=19.2cm
と求まります。答 19.2cm
以上
解答例2
水槽の底面積をS、水の容積をV、求める水深をhとします。
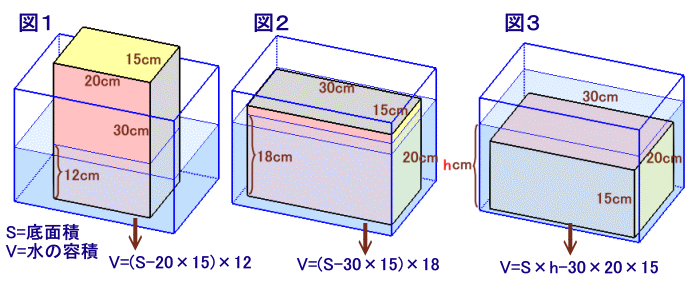
図1より、 V=(S−20×15)×12 ・・・ (1)
図2より、 V=(S−30×15)×18 ・・・ (2)
図3より、 V=S×h−30×20×15 ・・・ (3)
となります。(1)、(2)より、
(S−20×15)×12=(S−30×15)×18
S×6=30×15×18−20×15×12=4500
よって、S=4500÷6=750cm2となります。これを(1)に代入すると、
V=(750−300)×12=5400cm3
となります。従って、
h=(V+30×20×15)÷S
=(5400+9000)÷750=19.2cm
と求まります。