問題[推理]
|
|
|
|
|
|
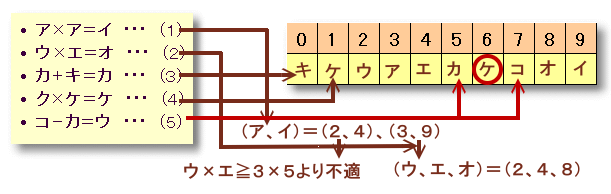
次の5つの式に使われているア、イ、ウ、エ、オ、カ、キ、ク、ケ、コの10個の文字には、 異なる文字にはそれぞれ違った整数があてはまるとき、ケにあてはまる数は何ですか?
|
|
|
|
|
|
解答例1[消去法 、とりあえずすべて決め]
| 長野 美光さん、Taroさん、受験勉強君さん、mhayashiさん、スマイルさん、 寺脇犬さん、ぺんこさん、bunさん、享平さん、りかさん、 多佳子さん、みっふぃー。さん、みかんさん、大岡 敏幸さん、たけのこさん、 パリンさん、HAJIさん、ふうきさん、kasamaさん、トシえもんさん、 tomhさん、高砂さん、きょろ文さん、アラちゃんさん、あす♪さん、 yytdvjvさん、吉田佳薫さん、中数さん、おさるさん、プーさん、いのさん、kobaさん、yutakaさん、高田一輝さん、 ゴンともさん、Nなヒトさん、吉田佳薫さん、他 |
(3)カ+キ=カより、キ=0
(4)ク×ケ=ケより、ケ≠0だから、ク=1
(1)ア×ア=イより、1桁の整数でアとイが異なる数になるのは、
(ア、イ)=(2、4)または(3、9)のとき。(ア、イ)=(2、4)のとき、0、1、2、4は既に決まっているので、
残りの数で最も小さい2数は3と5、
ところが、ウ×エ≧3×5=15となり(2)と矛盾。従って、(ア、イ)=(3、9)。
(2)ウ×エ=オより、積が1桁になるのは、(ウ、エ、オ)=(2、4、8)または(4、2、8)
ここまでで、残っている文字はカ、ケ、コの3個、残っている数字は、5、6、7の3個。
ウ=2または4なので、(5)コ−カ=2または4より、
(ウ、コ、カ)=(2、7、5)よって、最後に残ったの文字はケで、数字は6。
従って、ケ=6と求まります。答 6
以上