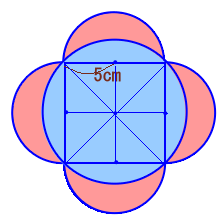
問題[平面図形]
|
|
|
|
|
|
|
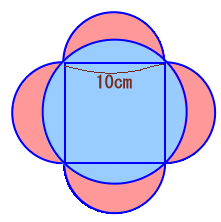 |
左図で、中心にある正方形の1辺が10cmのとき、 |
|
|
|
|
|
|
解答例1[(小円2個+正方形)−大円 、大円と半小円4個の面積は同じ、ヒポクラテスの三日月、全体と白円の面積の差、ひとつの赤い部分を4倍]
| カコモンコロシアムさん、たけのこさん、くくるさん、ゆうさん、 高田一輝さん、あまれっとさん、ぽっぽさん、kobaさん、HAJIさん、 パリンさん、うめこさん、ショウさん、kasamaさん、大岡 敏幸さん、 tomhさん、寺脇犬さん、アラちゃんさん、長野 美光さん、高砂さん、 多佳子さん、龍さん、藤井健洋さん、きょろ文さん、受験勉強君さん、Nなヒトさん、mmmさん、サザエさんさん、浜直君さん、yutakaさん、HAJIさん、maiさん、ゴンともさん、他 |
求める面積は、
(小円×2+正方形)−大円
となります。さて、
小円の面積=3.14×小円の半径2
大円の面積=3.14×大円の半径2
ですが、
大円の半径2=正方形の面積×1/2=小円の半径2×2
より、
小円の面積×2=大円の面積
となります。従って、
求める面積
=正方形の面積
=102
=100cm2
と求まります。答 100cm2
以上
(参考)ヒポクラテスの三日月
YOSHITA号船長室:数楽どん話(2)>ヒポクラテスの三日月
(その他の解法)
- 大円と小円4個の面積の比 ・・・きょろ文さん、他