問題[場合の数]
|
|
|
|
|
|
1の目が出ているサイコロがあります。 このサイコロをいずれかの横向きに倒します。 |
|
|
|
|
|
解答例1[2通り×4方向=8、 4通りX左右2方向X戻る1通り]
| カコモンコロシアムさん、高木謙一さん、パァ~子さん、ぺんこさん、みかんさん、 りかさん、たけのこさん、高田一輝さん、bunさん、ゆうさん、 HAJIさん、アラちゃんさん、kasamaさん、yutakaさん、うめこさん、 kobaさん、HAJIさん、elmotitiさん、くくるさん、SSSさん、 そうたさん、龍さん、BossFさん、きょんさん、理紗さん、 いのうえだいすけさん、yutakaさん、 浜直君さん、tekiさん、tomhさん、多佳子さん、 金さん、トシえもんさん、HAJIさん、他 |
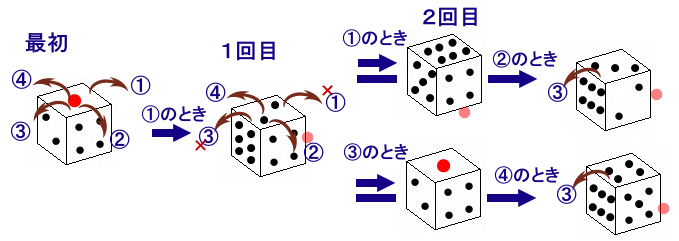
1回目に横に倒す方向は、①~④の4通りあります。
例えば①の方向に倒したときを考えてみましょう。
2回目に倒す方向も①~④の4通りありますが、
①のときは、1の目は真下にあるので、3回目に真上に来ることはできません。
②のときは、1の目は横にあるので、3回目に③の方向に倒すと真上に来ます。
③のときは、1の目は真上にあるので、3回目には横になってしまいます。
④のときは、1の目は真下にあるので、3回目に③の方向に倒すと真上に来ます。従って、2通り可能です。
1回目が②~④の場合も全く同様ですので、
合計2×4=8通り
と求まります。答 8通り
以上
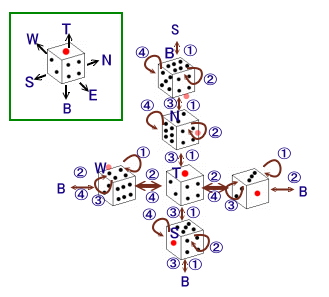
(参考)遷移図で表す
1の目が上を向いている状態をT、下を向いている状態をB、北を向いている状態をN、
東を向いている状態をE、南を向いている状態をS、西を向いている状態をWとします。
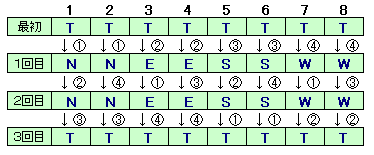
上図から、3回目にTの状態になるのは、 下表のように8通り。
(その他の解法)
- 群論(置換群) ・・・ゴンともさん、他
- 実験 ・・・享平さん、さるさん、他