第１１９問の解答

問題［推理]

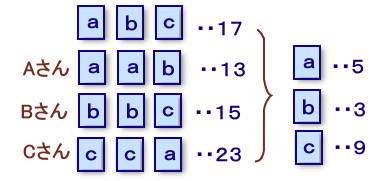
一桁の整数が書かれたカードが３枚あります。
A、B、Cの３人にこれらのカードを１枚ずつ配り、その数字を記録します。

このような作業を何回か行なった結果、Aが記録した数字の合計が １３、Bは１５、Cは２３になりました。
では、３枚のカードに書かれている数字は何でしょう？

解答例１[３枚の合計１７との差 ]

まるケンさん、カエルちゃまさん、kasamaさん、tomhさん、 雪猫さん、HAJIさん、梶本ヒロユキさん、他

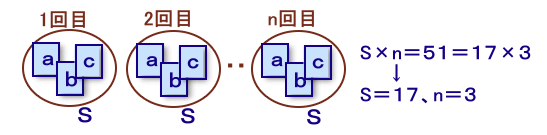
３枚のカードの数字をａ、ｂ、ｃ、これらの合計をＳとし、作業の回数をｎ回とします。

参考図１

３人が記録した数字の合計＝５１＝Ｓ×ｎとなりますので、Ｓ、ｎは５１の約数になります。
５１＝１７×３と表されますが、（Ｓ、ｎ）＝（１、５１）、（３、１７）、（５１、１）は題意に適しませんので、
（Ｓ、ｎ）＝（１７、３）となります。
従って、ａ＋ｂ＋ｃ＝１７　・・・　（１）

１人が合計３枚もらうカードの数字としては、
　（ア）３枚とも異なる
　（イ）３枚とも同じ
　（ウ）２枚が同じで１枚が異なる
の３通りがあります。

（ア）３枚とも異なるとき：
この３枚の数字合計＝ａ＋ｂ＋ｃ＝１７となりますが、数字合計が１７の人は誰もいませんので不適。

（イ）３枚が同じのとき：
数字の合計は３の倍数になりますので、このケースとしてはＢさんの１５しかあり得ません。
このとき、Ｂさんのカード＝１５÷３＝５となりますので、
　残りの２種類の数字計＝１７−５＝１２となります。
従って、ａ＝５とすると、ｂ＋ｃ＝１２と言うわけです。
Ａ、Ｃさんとも２枚が同じで１枚が異なることになるので、
　Ａさん：ｂ＋ｂ＋ｃ＝１３
　Ｃさん：ｃ＋ｃ＋ｂ＝２３
より、ｂ＝１、ｃ＝１１を得ますが、カードの数字は１桁なので不適。

（ウ）２枚が同じで１枚が異なる：結局３人ともこのケースになります。よって、
Ａさん：ａ＋ａ＋ｂ＝１３　・・・　（２）
Ｂさん：ｂ＋ｂ＋ｃ＝１５　・・・　（３）
Ｃさん：ｃ＋ｃ＋ａ＝２３　・・・　（４）
ということになります。

参考図２

（１）−（２）より、ｃ−ａ＝１７−１３＝４、ｃ＝ａ＋４
（１）−（３）より、ａ−ｂ＝１７−１５＝２、ａ＝ｂ＋２、よってｃ＝ｂ＋６

（１）に代入して、
　（ｂ＋２）＋ｂ＋（ｂ＋６）＝１７
よって、
　ｂ＝（１７−２−６）÷３＝３
　ａ＝３＋２＝５
　ｃ＝３＋６＝９
と求まります。

答　 ３、５、９

以上

解答例２[３枚の合計１７との差（別解）]

HAJIさん、他

Ｓ＝１７、n＝３までは解答例１と同じ。

さて、３枚の数字合計＝１７＝奇数なので、これに着目すると、
　偶数＋偶数＋奇数＝１７
　奇数＋奇数＋奇数＝１７
の２通りが考えられます。

１桁の数字の中から該当するものを抜き出すと、
　（１、７、９）、（２、６、９）、（３、５、９）、（２、７、８）、（３、６、８）、（４、５、８）、（４、６、７）
の７ケースが考えられます。

これらのうち、題意を満たすものを探してみると、
　（３、５、９）のみになります。
　

（その他の解法）