第１２０問の解答

問題［平面 図形]

問題図

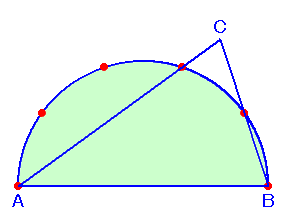左図は、ABを直径とする半円と、△ABCを重ねたものです。

赤色の点が、半円上に等間隔にならべてあるとき、∠Cは何度になりますか？

解答例１[△ABCが二等辺三角形 、円周角2発+、10角形から順を追って、180-(90+18)]

ゴンともさん、始 受験勉強君さん、ショウさん、HAJIさん、bunさん、 kasamaさん、tomhさん、kobaさん、 　ゴンともさん、龍さん、浜直君さん、 　tymさん、ψ（プサイ）さん、 　きょろ文さん、他

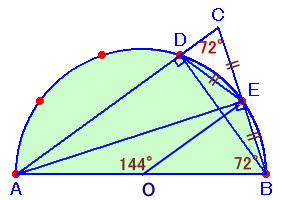
円の中心をO、赤い点のうちAC上のものをD、BC上のものをEとします。

参考図１

∠AEB＝∠AEB＝１８０°÷２＝９０°（半円周に対する円周角）、
従って、△BCDは∠BCD＝９０°の直角三角形となります。

また、∠ABE＝∠AOE÷２＝１８０°×４/５÷２＝７２°（弧AEに対する円周角）

さて、弧DE＝弧BEより、DE＝EB、
よって、Eは直角三角形BCDの斜辺BC上にある点だから、BCの中点。

すると、EはAからBCに下ろした垂線の足で、しかもBCの中点ということだから、
△ABCはAB＝ACの二等辺三角形になります。

従って、
　∠C＝∠ABE＝７２°
と求まります。

答　７２°

以上

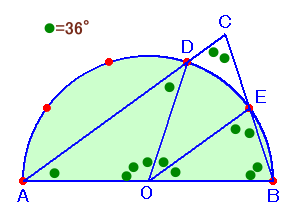
解答例２[36×2、補助線を引 く、９０×４÷５]

たけのこさん、R.Tさん、　波ピカさん、　mhayashiさん、heroさん、他

θ＝１８０°÷５＝３６°とします。１８０°＝θ×５。

参考図２

△OADは、OA＝ODの二等辺三角形で、∠AOD＝θ×３、
よって、∠ＯＡＤ＝∠ＯＤＡ＝（１８０°−θ×３）÷２＝θ

また、△OＢＥは、OＢ＝OＥの二等辺三角形で、∠ＢOＥ＝θ、
よって、∠ＯＢＥ＝∠ＯＥＢ＝（１８０°−θ）÷２＝θ×２

従って、
　∠ＡＣＢ＝１８０°−∠ＯＡＤ−∠ＯＢＥ
　　　　　＝θ×５−θ−θ×２
　　　　　＝θ×２＝７２°
と求まります。

（その他の解法）