第１２２問の解答

問題［速さの問題]

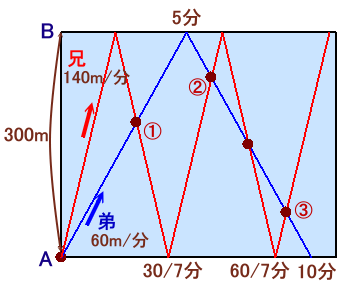
３００ｍ離れたA.、B、２つの地点の間を、兄が自転車に乗って毎分１４０ｍの速さで、弟は毎分６０ｍの速さで歩いています。
２人がともにA地点を同時に出発して何往復かしていると、途中で２人が同じ場所にくることが何回か出てきます。
２人の場所が５回目（スタートの際を含める）に同じになるのは、出発から何分後のことですか？

解答例１[図と頭をつかう、旅人算２式の合わせ技]

享平さん、あさみさとしさん、kasamaさん、高田一輝さん、tomhさん、たけのこさん、雪猫さん、きょろ文さん、
カコモンコロシアムさん、HAJIさん、HAJIさん、shuさん、北島正一さん、他

ダイアグラムで考えましょう。

参考図１

弟は、６０m/分で進むので、AB間を６００m÷６０m/分＝１０分で往復します。
一方兄は、１４０m/分で進むので、AB間を６００m÷１４０m/分＝３０/７分で往復します。
従って、６０/７≒８．５７...分で２往復します。

これらから、出発して１０分間に兄は弟と、３回行き違い、１回追越すことになります。
従って、出発時を含めて５回目に２人が同じ位置にいるのは、ちょうど３回目に行き違うときになります。

２人が１回行き違うのは、２人の進んだ距離の合計がABを１往復するときなので、
　所要時間＝６００m÷（１４０m/分＋６０m/分）＝３分

従って、３回目に行き違うのは、３分×３＝９分後になります。

答　 ９分後

以上

（その他の解法）