問題[推理]
|
|
|
|
|
|
A、B、C、D、Eの5枚のくじがあります。当たりくじは1等、2等、3等が1枚ずつです。
このとき、当たりくじはどのくじでしょうか。1等、2等、3等の順に答えてください。 |
|
|
|
|
|
解答例1[2→3→1で3人確定→2→1で順位確定]
| カコモンコロシアムさん、他 |
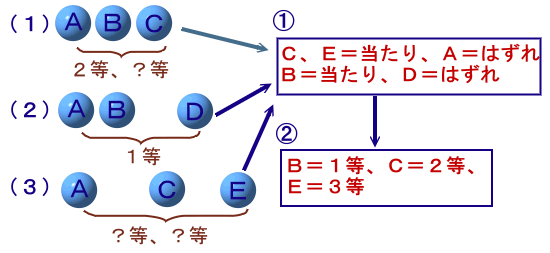
まず当たりくじを確定し、次にそれぞれの順位を決めていきます。
(ステップ①)
(2)より、残ったC、E=当たりと分かります。
すると、(3)よりA=はずれとなるので、(1)からB=当たりと分かります。以上より、B、C、E=当たり、A、D=はずれとなります。
(ステップ②)
(2)より、B=1等と分かります。
すると、(1)よりC=2等となるので、(3)からE=3等と分かります。答 B、C、E
以上
解答例2[1,2番目の条件から・・・、論理論証]
| 高田一輝さん、上中天博さん、tomhさん、雪猫さん、HAJIさん、 SSSさん、たけのこさん、mmmさん、他 |
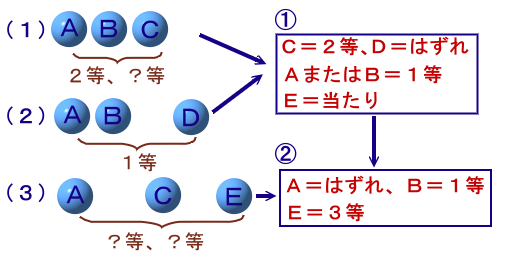
(ステップ①)
(1)、(2)より、CがDに替わることでが2等の当たりくじ1個が減ったことから、
C=2等、D=はずれが分かります。
従って、(2)よりA=1等、B=はずれ、またはA=はずれ、B=1等となります。すると、A、B、C、Dの4人の中には、当たりが2 枚しかいないことになるので、残ったE=当たりと分かります。
(ステップ②)
ステップ①より、C、Eが当たりとなったので、(3)より、A=はずれが分かります。
ステップ①より、AまたはB=1等だったので、B=1等と分かります。
再度ステップ①より、C=2等と決まっていたので、残るE=3等と分かります。
解答例3[1等を考える]
| hiroさん、他 |
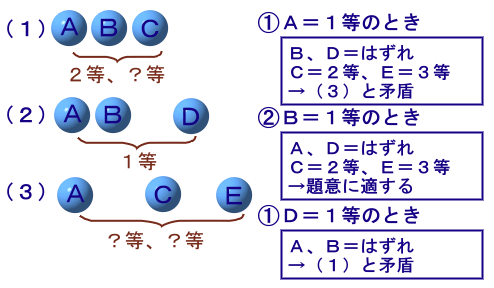
(2)よりA、B、Dのいずれかが1等となります。
①A=1等のとき
(2)より、残るB、D=はずれとなります。
(1)より、残るC=2等となります。
すると、残ったE=3等となりますが、A、C、Eの3人が当たりは、(3)と矛盾しますので不適。②B=1等のとき
(2)より、残るA、D=はずれとなります。
(1)より、残るC=2等となります。
すると、残ったE=3等となりますが、これらは(1)、(2)、(3)のいずれの条件も満たすので、題意に適します。①D=1等のとき
(2)より、残るA、B=はずれとなります。
すると(1)より、A、B、Cのうち当たりはCの1枚となり不適。
(その他の解法)
- 題意の3条件の組み合わせ ・・・ ゴンともさん、川村高雅さん、ショウさん、あさみさとしさん、北島正一さん、 みかんさん、N.Nishiさん、パリンさん、浜直君さん、kasamaさん、 スーパーモリオさん、まゆちゃんさん、 石田晃貴さん、他多数
(1)より、A、B、Cのうち2個が当たり・・・3通り、(2)よりA、B、Dのうち1個が当たり・・・3通り、(3)よりA、C、Eの中2個が当たり・・・3通り
これらを組み合わせ3×3×3=27通りより題意に適するものを探す