問題[平面図形]
|
|
|
|
|
|
|
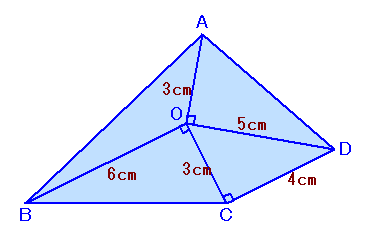 |
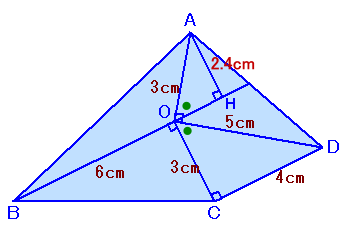
左図の四角形ABCDの面積は何cm2ですか? |
|
|
|
|
|
|
解答例1[三角形OABの高さは2.4cmとわかる、三角形OCDの相似を作る]
| カコモンコロシアムさん、いのうえだいすけさん、HAJIさん、kasamaさん、きょろ文さん、 始 受験勉強君さん、5.12さん、たけのこさん、エニグマ さん、北島正一さん、 他 |
AからBOの延長線に下ろした垂線の足をHとします。
∠AOB+∠COD=360°−(∠AOD+∠BOC)=360°−90°×2=180°
よって、∠AOH=180−∠AOB=∠COD、
従って、△AOHは△DOCと相似な直角三角形となります。よって、AH=AO×DC/OD=3×4/5=2.4cm
従って、
四角形ABCD
=△ABO+△BOC+△COD+△DOA
=1/2×6×2.4+1/2×6×3+1/2×3×4+1/2×5×3
=7.2+9+6+7.5
=29.7cm2
と求まります。答 29.7cm2
以上
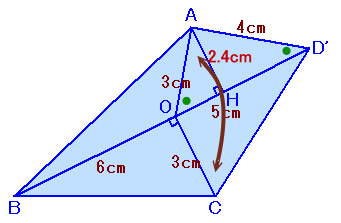
解答例2[四角形OACDを裏返す 、三角形OCDを裏返す]
| mhayashiさん、N.Nishiさん、SSSさん、オリガツさん、HAJIさん、 他 |
四角形AOCDを裏返して、AとCが入れ替わるようにしたものを四角形COAD’とします。
∠AOB+∠AOD’=∠AOB+∠COD=180°より、B、O、D’は一直線上に並びます。
AからBD’に下ろした垂線の足をHとすると、△AOHと△D'OAは相似だから、
AH=AO×AD’/OD’=3×4/5=2.4cmよって、
四角形ABCD
=△ABD’+△BCD’
=1/2×11×2.4+1/2×11×3
=1/2×11×5.4
=29.7cm2
と求まります。
(その他の解法)
- 三角関数 ・・・ ゴンともさん、tymさん、tomhさん、 他
△AOB=3*6*sin(∠AOB)/2、sin(∠AOB)=sin(180°-∠COD)=4/5