問題[割合]
|
|
|
|
|
|
箱の中に赤と白のカードがそれぞれ何枚か入っています。 カードをすべて箱に戻したあと、今度は1回に赤のカードを2枚ずつ、白のカードを3枚ずつ取り出したところ、 はじめ、この箱の中には赤と白のカードは合計何枚入っていましたか。 |
|
|
|
|
|
解答例1[比で考える 、白を6個単位で考える]
| カコモンコロシアムさん、高田一輝さん、あさぱぱさん、しゅさん、bunさん、 まるケンさん、HAJIさん、オリガツさん、W~亜依の唄さん、他 |
白いカードは、2枚ずつ取り出したときも、3枚ずつ取り出したときも、ちょうどなくなったことから、
枚数は、2および3の倍数、すなわち6の倍数となります。そこで、白いカードは6枚単位で何組あるかを求めてみましょう。
1回目では、白いカードを2×3=6枚ずつ取り出すと考えると、赤いカードは3×3=9枚ずつ取り出して8枚余ることになります。
そして、2回目には白いカードを3×2=6枚ずつ取り出すと考えると、赤いカードは2×2=4枚ずつ取り出して43枚余ることになります。
2回目は1回目に比べて、赤いカードを9−4=5枚ずつ少なく取り出すので、
取り出す回数=(43−8)÷5=7回となります。従って、
白いカードは6枚×7組=42枚
赤いカードは9枚×7組+8枚=71枚
合計=42+71=113枚
と求まります。答 113枚
以上
解答例2[連立方程式]
| 日付変更人さん、tymさん、ふうきさん、tomhさん、ゴンともさん、 N.Nishiさん、りかさん、寺脇犬さん、Plutonianさん、kasamaさん、 milkさん、 他 |
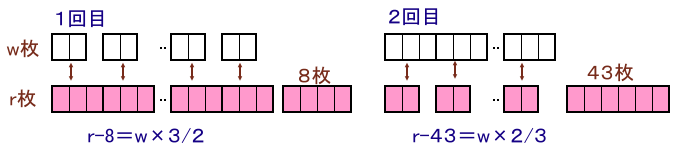
白いカードがw枚、赤いカードがr枚あったとします。
1回目の操作より、
r−8=w×3/2 ・・・ (1)2回目の操作より、
r−43=w×2/3 ・・・ (2)(1)−(2)より、
35=w×5/6
w=35×6/5=42枚従って(1)より、
r=42×3/2+8=71枚よって、
合計枚数=42+71=113枚
と求まります。