問題[速さの問題]
|
|
|
|
|
|
P地点とQ地点を結ぶまっすぐな道を、寅さんと入鹿君がP地点を同時に出発して、二人とも休むことなくPQ間を2往復しました。 |
|
|
|
|
|
解答例1[2人が一定時間に進む距離の比から求める]
| カコモンコロシアムさん、takaさん、bunさん、HAJIさん、高田一輝さん、 kasamaさん、ゆうさん、S0さん、寺脇犬さん、他 |
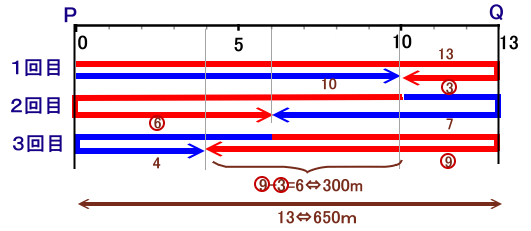
下図のような線分図で考えます。
PQ間の距離を13とします。
2人が分かれて次に出会うまでに、2人が進む合計距離は、PQ間を往復する26。
2人の速度比は8:5だから、それぞれが進んだ距離は、
寅さん=26×8/(8+5)=16
入鹿君=26×5/(8+5)=10
となります。すなわち、寅さんは出会うまでに(片道+3)だけ進むことになります。
従って、出発して出会うまでに寅さんが進む距離は、
1回目:(片道+3)×1=片道×1+3
2回目:(片道+3)×2=片道×2+6
3回目:(片道+3)×3=片道×3+9
4回目:(片道+3)×4=片道×4+12 ←寅さんは2往復を終えているので不適よって、2人が出会うのは3回ということになります。
出会う地点は、
1回目:Qから3の地点
3回目:Qから9の地点
となり、これらの距離は、9−3=6となります。これが300mなので、PQ間の13は、
PQ=300m×13/6=650m
と求まります。答 650m
以上
解答例2[ダイヤグラムと三角形の相似を使っての比]
| N.Nishiさん、Picoさん、みかんさん、tomhさん、Plutonianさん、 KIMOさん、他 |
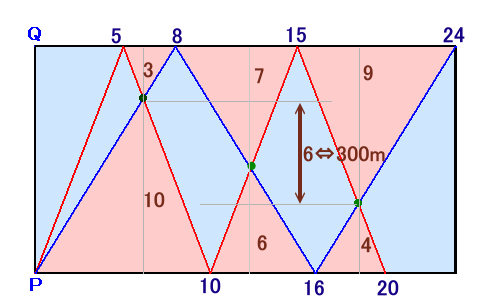
下図のようなダイアグラムで考えます。赤い部分の三角形は全て相似です。
2人の速度比は8:5だから、PQ片道に要する所要時間の比は5:8となります。
最初にPに到達するまでの時間は、寅さん=5、入鹿君=8、差=3、
寅さんがPQを往復してPに帰るまでに5×2=10だけ要するので、
最初の赤い三角形の相似比は3:10なので、QとPを3:10で分ける地点です。同様に、2回目はQとPを7:6で分ける地点、3回目はQとPを9: 4で分ける地点になります。
以下、解答例1と同じ。
(その他の解法)
- 全体を8ブロックに分ける ・・・ ゴンともさん、他