問題[場合の数]
|
|
|
|
|
|
1、2、3、・・・と順に1000までの整数をすべて書いたとき、数字の1は何回書くことになりますか |
|
|
|
|
|
解答例1[各位の1の数を足す 、000から999まで数字は同数]
| Plutonianさん、カコモンコロシアムさん、ふうきさん、HAJIさん、kasamaさん、 きっしんさん、kobaさん、ミッキーさん、高田一輝さん、鳳 ナオさん、ちず さん、寺脇犬さん、長野 美光さん、 Picoさん、まるケンさん、他 |
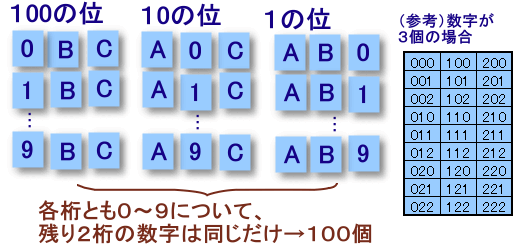
000から999までを考えます。(0は省略しないで表示)
100の位:0〜9の各数字について、10の位、1の位はそれぞれ0〜9の10個ずつ ・・・ 100個
10の位:0〜9の各数字について、100の位、1の位はそれぞれ0〜9の10個ずつ ・・・ 100個
1の位:0〜9の各数字について、100の位、10の位はそれぞれ0〜9の10個ずつ ・・・ 100個
よって、どの数字も同じ100個ずつ、合計300個。
従って、1の数字も合計300個であることが分かります。さて、最初の000は対象外ですが、これには1の数字がありません。
また、数えていなかった1000には1の数字が1個あります。よって、0001から1000では、1を301回書くことになります。
答 301回
以上
解答例2[2桁までに1の数を元に3桁を考える]
| ゴンともさん、tymさん、みかんさん、他 |
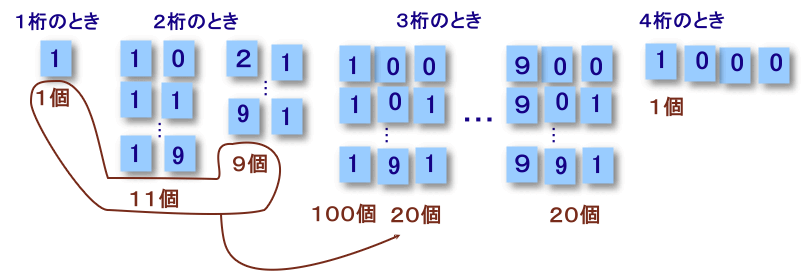
1桁のとき ・・・ 1の1個
2桁のとき ・・・ 10、11、・・・、19の10個
21、31、・・・、91の9個 計19個
3桁のとき ・・・ 100、101、・・・、199の100+20=120個
201、210、・・・、291の20個
301、310、・・・、391の20個
・・・
901、910、・・・、991の20個 計120+20×8=280個
4桁のとき ・・・ 1000の1個
従って、
合計=1+19+280+1=301個
と求まります。
(その他の解法)
- 組み合わせ ・・・ N.Nishiさん、多佳子さん、他
まず4桁は 1000 だけで 1個
あとは3桁で
☆1を1つだけ使う場合 1□□ □1□ □□1 の3通り
□にはそれぞれ 0,2,3,4,5,6,7,8,9の9通り考えられるので まとめて9×9×3(個)
☆1を2つ使う場合 11□ 1□1 □11 の3通り で 同様に 9×3(通り)×2(個)
☆1を3つ使う場合 111 の1通りで 1×3(個)
よって 1+243+54+3=301(個)