第１３３問の解答

問題［平面図形]

問題図

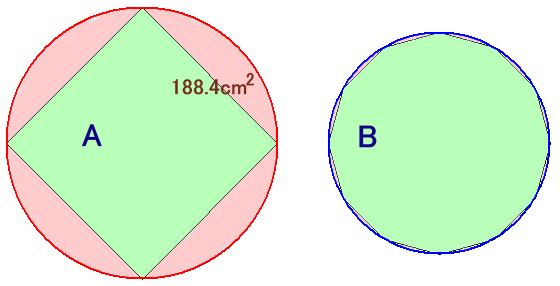左図のA.Bは面積の等しい正方形と正十二角形です。
Aに外接する円(Aの周りをちょうど囲む)の面積が188.4cm2のとき、 Bに外接する円の面積は、何cm2になりますか？

解答例１[sin30°＝1/2 の利用 、半径×半径×３の利用、√、外接円の半径、 同円内の場合の逆比、面積比の利用]

Plutonianさん、ゴンともさん、N.Nishiさん、tomhさん、多佳子さん、 kasamaさん、Ｓ０さん、高田一輝さん、HAJIさん、Picoさん、yonedaさん、yoiさん、凱龍さん、寺脇犬さん、allpassさん、Taroさん、他

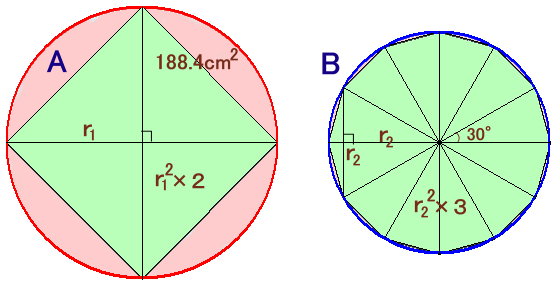
Aに外接する円の半径をｒ1、Ｂに外接する円の半径をｒ2とします。

参考図１

Aの円の面積＝３．１４×ｒ12＝１８８．４cm2より、
　ｒ12＝１８８．４÷３．１４＝６０

題意より、
　Ａの正方形の面積＝１/２×ｒ12×４＝ｒ12×２＝１２０cm2
　Ｂの正１２角形の面積＝１/２×ｒ2×（１/２×ｒ2）×１２＝ｒ22×３＝１２０cm2

従って、
　Ｂの円の面積＝３．１４×ｒ22＝３．１４×４０＝１２５．６cm2
と求まります。

答　 １２５．６cm2

以上