問題[平面図形 (整数の性質)]
|
|
|
|
|
|
|
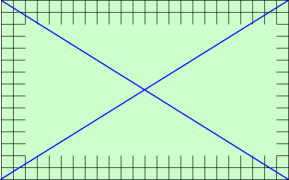 |
1辺が1cmの正方形の形をした紙が360枚あります。 この紙を、たて 15cm、よこ24cmの長方形の形にすきまなくならべ、長方形の対角線で、図の青線のように2度切断しました。 このとき2枚以上に切断される正方形の紙は、360枚中何枚ありますか? |
|
|
|
|
|
|
解答例1[実際に作図 、5X8 の部分で12個。、 たて+横−最大公約数、互いに素の関係]
| N.Nishiさん、HAJIさん、ゴンともさん、高田一輝(姉小路)さん、tomhさん、 kasamaさん、みかんさん、スモークマンさん、長野 美光さん、さとちゃんさん、ぷーさん、理紗さん、他 |
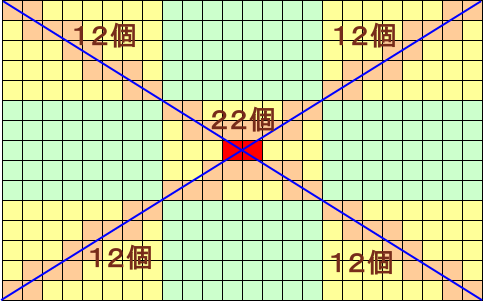
実際に作図してみます。
15と24の最小公倍数は3なので、縦15cm×横24cmの長方形は、縦5cm×横8cmの長方形9個に分割して考えることができます。
切断される正方形の数は、4隅の4個が12個、真ん中の1個が22個(12×2−2と数えることもできます)、
従って、12×4+22=70個と求まります。答 70個
以上