問題[平面図形]
|
|
|
|
|
|
|
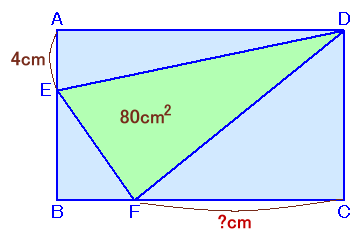 |
左図の長方形ABCDの面積が216cm2、三角形DEFの面積が80cm2、AEの長さが4cmのとき、CFの長さは何cmになりますか? |
|
|
|
|
|
|
解答例1[3つの直角三角形の面積の2倍と長方形の面]
| 算数一発さん、rikaさん、優太さん、他 |
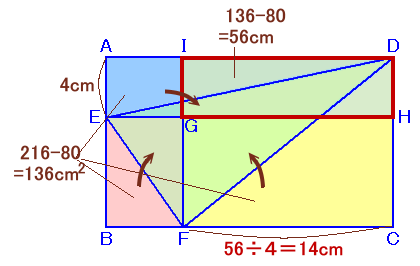
Eを通って辺BCと平行に引いた直線とCDとの交点をH、Fを通って辺BAと平行に引いた直線とADとの交点をI、
およびEHとFIの交点をGとします。
△AED+△EBF+△DFC
=長方形ABCD−△DEF
=216−80=136cm2△DEH=△AED、△EFG=△EBF、△IFD=△DFCより、
△DEH+△EFG+△IFD
=△AED+△EBF+△DFC
=136cm2△DEH+△EFG+△IFD−△DEF
=長方形IGHD
=136−50=56cm2よって、
FC=GH=56÷4=14cm
と求まります。答 14cm
以上
解答例2[ADF=108c㎡を利用、FからADに垂線を下ろして]
| ドイルさん、宮前俊司さん、16わんさん、ろろさん、Taroさん、まるケンさん、他 |
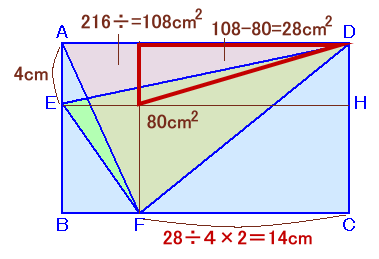
△AFD−△EDF=△AED−△AEF=1/2×AE×FC
△AFD=長方形ABCD÷2=108cm2
△EDF=80cm2
AE=4cmよって、
108−80=1/2×4×FC従って、
FC=28÷4×2=14cm
と求まります。
(その他の解法)
- 方程式を用いて解く ・・・ N.Nishiさん、ゴンともさん、鳳 ナオさん、tomhさん、龍さん、 寺脇犬さん、多佳子さん、宮前俊司さん、マサ5599さん、たこ焼きbさん、 ふうきさん、他
- 三角形の移動、等積変形 ・・・ xxx1234さん、kasamaさん、bunさん、龍さん、 他
- 面積の差が高さの差 ・・・ HAJIさん、他
- 面積比 ・・・ 高田一輝(姉小路)さん、他