問題[平面図形]
|
|
|
|
|
|
|
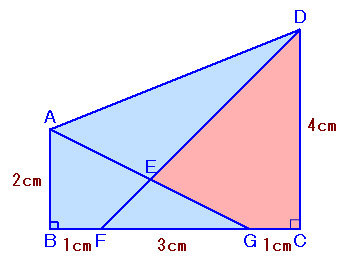 |
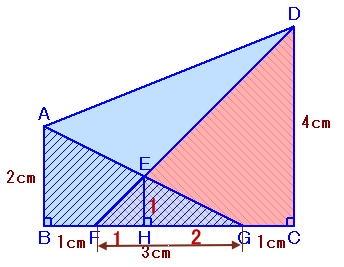
左図のABCDは∠Bと∠Cが直角の台形で、AB=2cm、BF=1cm、FG=3cm、GC=1cm、CD= 4cmとなっています。 このとき、四角形EGCDの面積は何cm2になりますか? |
|
|
|
|
|
|
解答例1[EからFGに垂線を引き相似を利用]
| bunさん、N.Nishiさん、高田一輝(姉小路)さん、あまれっとさん、皆我ポさん、 kasamaさん、Dr.Sさん、にっしーさん、りかさん、多佳子さん、他 |
点Eから辺BCに下ろした垂線の足をHとします。
△EHGと△ABGは相似より、
EH:HG=AB:BG=2:4=1:2 ・・・ (1)△EFHと△DFCは相似より、
EH:FH=DC:FC=4:4=1:1 ・・・ (2)(1)、(2)より、
EH:FG=1:3FG=3cmだから、EH=1cmとなります。
従って、
四角形DEGC
=△DFC−△EFG
=1/2×FC×DC−1/2×FG×EH
=1/2×4×4−1/2×3×1
=13/2
=6.5cm2
と求めることができます。答 6.5cm2
以上
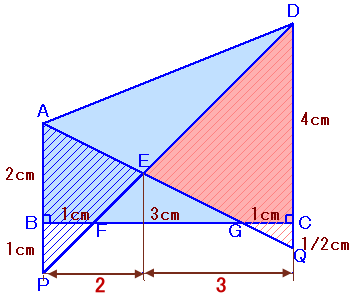
解答例2[三角形の相似を使う 、補助線を引き相似を使う]
| ちずさん、こえだ§さん、みかんさん、スモークマンさん、アセアセさん、 いっひーさん、HAJIさん、他 |
ABとDFの延長線の交点をP、DCとAGの延長線の交点をQとします。
△PFBと△DFCは相似より、
BP:BF=DC:FC=4:4=1:1
よって、
BP=BF=1cm△QGCと△AGBは相似より、
QC:GC=AB:GB=2:4=1:2
よって、
QC=GC×1/2=1/2cmまた、△AEPと△QEDは相似で、
相似比=AP:DQ=3:9/2=2:3
よって、
△QEDで、Eからの高さ=3cmとなります。従って、
四角形DEGC
=△QED−△QGC
=1/2×9/2×3−1/2×1×1/2
=26/4
=6.5cm2
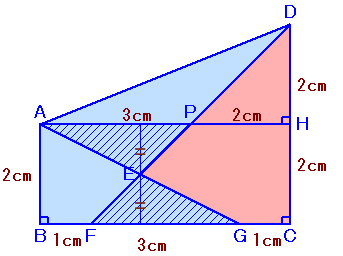
解答例3[等しい三角形を考える(合同)]
| あっけらけさん、マサ5599さん、mieさん、他 |
点Aから辺DCに下ろした垂線の足をHとし、AHとDFの交点をPとします。
HC=AB=2cm、DH=DC−HC=2cmとなります。
すると、△DPHと△DFCは相似より、
PH:DH=FC:DH=2:2=1:1
よって、
PH=DH=2cm
となります。従って、AP=AH−PH=BC−PH=5−2=3cm
△EFGと△EPAは相似で、かつFG=APより合同、
よって、△EFGの高さ=AB×1/2=1cmと分かります。以下、解答例1と同様。
(その他の解法)
- 座標置き ・・・ ゴンともさん、tomhさん、まるケンさん、他
方程式を解いて直線AGとFDの交点の座標を求める
- タンジェントを使う
・・・ ハラギャーテイさん、他