問題[場合の数]
|
|
|
|
|
|
サイコロを3回振ります。 |
|
|
|
|
|
解答例1[愚直にすべて、 二つを選んで、樹形図]
| ゴンともさん、多佳子さん、HAJIさん、おだのぶながさん、優太さん、 mieさん、kobaさん、tomhさん、とマティさん、tamagonnさん、 Dr.Sさん、【UU】亜依の唄さん、ティンクさん、高田一輝(姉小路)さん、龍さん、N.Nishiさん、長野 美光さん、ナッパさん、他 |
3回振ってサイコロの出た目の数を、x、y、zとおきます。
題意より、
x+y+z=12(ただし、1≦x、y、z≦6)
を満たします。3変数だと分かりにくいので、zを固定し、
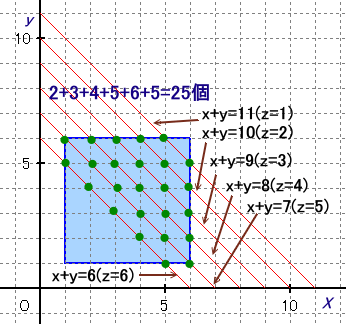
x+y=12−z(ただし、6≦12−Z≦11)
を満たす(x、y)の組を数えます。
z=1のとき:x+y=11→(x、y)=(5、6)、(6、5) ・・・ 2通り
z=2のとき:x+y=10→(x、y)=(4、6)、(5、5)、(6、4) ・・・ 3通り
z=3のとき:x+y=9→(x、y)=(3、6)、(4、5)、(5、4)、(6、3) ・・・ 4通り
z=4のとき:x+y=8→(x、y)=(2、6)、(3、5)、(4、4)、(5、3)、(6、2) ・・・ 5通り
z=5のとき:x+y=7→(x、y)=(1、6)、(2、5)、(3、4)、(4、3)、(5、2)、(6、1) ・・・ 6通り
z=6のとき:x+y=6→(x、y)=(1、5)、(2、4)、(3、3)、(4、2)、(5、1) ・・・ 5通り
従って、
合計=2+3+4+5+6+5=25通り
と求まります。答 25通り
以上