問題[割合]
|
|
|
|
|
|
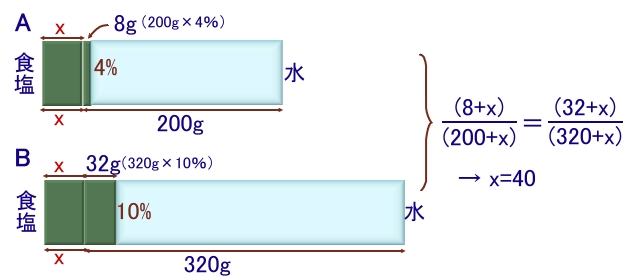
4%の食塩水が200gと、10%の食塩水が320gあります。 |
|
|
|
|
|
解答例1[方程式 、水の重さに着目した方程式、比、方程式&因数分解(?)]
| ゴンともさん、takaさん、tymさん、高田一輝(姉小路)さん、 あけらけさん、kasamaさん、多佳子さん、パァ〜子さん、Plutonianさん、 N.Nishiさん、大岡 敏幸さん、tomhさん、オーレンジャーさん、鳳 ナオさん、mieさん、まーくんさん、ドイルさん、ハリケンジャーさん、kobaさん、寺脇犬さん、ローリーさん、エミリーさん、SPDさん、他 |
最初4%だった食塩水をA、10%だった食塩水をBとします。
加えた食塩の量をxgとおいて方程式を考えます。
最初のA:食塩の量=200g×4%=8g、
水の量=200−8=192g
→ xgの食塩を加えた後の濃さ=(8+x)/(200+x)×100 %最初のB:食塩の量=320g×10%=32g、
水の量=320−32=288g
→ xgの食塩を加えた後の濃さ=(32+x)/(320+x)×100 %従って、
(8+x)/(200+x)=(32+x)/(320+x) ・・・ (1)
(8+x)(320+x)=(32+x)/(200+x)
x2+328x+2560=x2+232x+6400
よって、
x=(6400−2560)/(328−232)=40g
と求まります。あるいは、(1)より、
(200+x)/(8+x)=(320+x)/(32+x)
(192+8+x)/(8+x)=(288+32+x)/(32+x)
192/(8+x)+1=288/(32+x)+1
288/192=(32+x)/(8+x)
(96+192)/192=(24+8+x)/(8+x)
96/192+1=24/(8+x)+1
8+x=192×24/96=192×1/4=48
よって、
x=48−8=40g
を得ます。答 40g
以上
解答例2[食塩と食塩水の量の差に着目、水の重さに着目したけど方程式は使わず、比を利用した計算 、比]
| HAJIさん、メガレンジャーさん、まるケンさん、デカレンジャーさん 、エミリーさん、SPDさん、HYさん、他 |
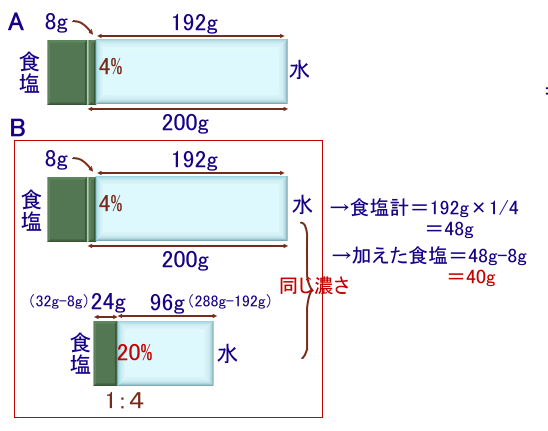
食塩水BとAの差を考えます。
差の食塩の量=32g−8g=24g、
水の量=288g−192g=96g食塩を加えた後のAとBの濃さが等しくなることから、
差の食塩水の濃さ20%と、食塩を加えた後のAの濃さは等しいことになります。従って、
食塩を加えた後のAの食塩の量=192×1/4=48g
よって、
加えた食塩の量=48g−8g=40gとなります。、
(その他の解法)
- 面積図 ・・・ bunさん、カーレンジャーさん、 他
食塩は100%の食塩水と考えて比を使用して解く?