問題[平面図形]
|
|
|
|
|
|
|
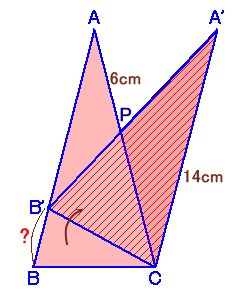 |
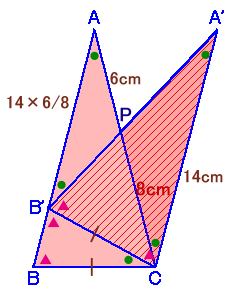
左図のように、AB=AC=14cmの二等辺三角形を、頂点Cを中心にして回転させ、 このときのACとA'B'の交点をPとしたとき、AP=6cmになっていました。 |
|
|
|
|
|
|
解答例1[ABとA'Cが平行 、各辺の相似。、二等辺三角形と相似の利用]
| ゴンともさん、高田一輝(姉小路)さん、ちずさん、bunさん、藤井 拓人さん、 みかんさん、スモークマンさん、N.Nishiさん、tamagonnさん、kasamaさん、エミリーさん、HAJIさん、elmotitiさん、みやもーぷんぽさん、tomhさん、 多佳子さん、マリオさん、鉄アニさん、yutakaさん、他 |
∠BAC=α、∠ABC=∠ACB=βとします。
△PAB'と△PA'Cは、∠PAB'=∠PA'C=α、∠APB'=∠PA'C(対頂角)より、相似となります。
さらに、これらが二等辺三角形になることを示しましょう。BC=B'Cより、△CB'Bは二等辺三角形となります。
従って、
∠CB'B=∠CBB'=β ・・・ (1)
となります。従って、∠BB'C=∠A'CB'より、ABとA'Cは錯角が等しいので平行、
よって、∠PB'A'=∠PA'C=α、∠PCA'=∠PAB'=α(錯角)より、
△PAB'と△PA'Cは、ともに底角がαの二等辺三角形と分かります。従って、
△APB'と△PCA'は相似で相似比=AP:PC=6:8、
AB'=A'C×6/8=14×6/8=21/2=10.5cm
よって、
BB'=14−10.5=3.5cm
と求まります。答 3.5cm
以上
(△PAB'と△PA'Cが二等辺三角形を示す別解)
(1)より、
∠B'CB=180°−∠CB'B−∠CBB'=α
よって、
∠A'CP=∠A'CB'−∠PCB'=∠ACB−∠PCB'=∠B'CB=α従って、△PA'Cは底角がαの二等辺三角形と分かります。
△PAB'と△PA'Cは相似だから、△PAB'も底角がαの二等辺三角形。
(その他の解法)
- 三角関数 ・・・ ハラギャーテイさん、kjhkさん、他