問題[平面図形]
|
|
|
|
|
|
|
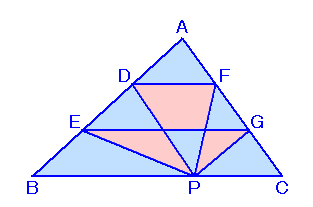 |
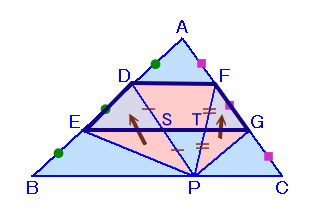
左図は、面積が36cm2の△ABCです。 では、赤色をつけた部分の面積の合計は何cm2でしょうか? |
|
|
|
|
|
|
解答例1[相似を使う、等積変形、スマートに解くとは・・・]
| HAJIさん、まーくんさん、ゴンともさん、村岡陽さん、阪急大好き!さん、 ひろさん、R.Tさん、Dr.Sさん、スモークマンさん、ヒデさん、 tamagonnさん、tomhさん、かいとのパパさん、多佳子さん、あすーるさん、 パリンさん、N.Nishiさん、ヌオさん、Plutonianさん、村岡陽さん、あけらけさん、 tymさん、琉雅パパさん、鉄アニさん、bunさん、 みかんさん、kasamaさん、mhayashiさん、高田一輝(姉小路)さん、英之さん、他 |
EGとPDの交点をS、PFの交点をTとします。
辺DF、EGは底辺BCと平行、
よって、△DBPについて中点連結定理より、DS=SP、
従って、△EPS=△DES。同様に、△TPG=△FTG。
従って、
求める面積
=台形DEGF=△AEG−△ADF
=(2/3)2×△ABC−(1/3)2×△ABC
=1/3×△ABC=1/3×36=12cm2
と求まります。答 12cm2
以上
(その他の解法)
- 具体的に長さを決めて面積を計算 ・・・ パァ〜子さん、他