問題[場合の数]
|
|
|
|
|
|
|
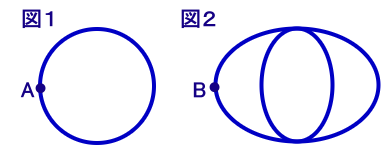 |
図1のような図形を、点Aを出発点として一筆書きする方法は2通りあります。 では、図 2のような図形を、点Bを出発点として一筆書きする方法は何通りありますか? |
|
|
|
|
|
|
解答例1[3×2×2、2*3*2、3*2の倍 、2*2*3、場合分け、書き出し]
| ふうきさん、太陽の陽さん、大西将也さん、tymさん、ゆうsukeさん、 hitoshiさん、みかんさん、kaizerさん、ゴリさん、N.Nishiさん、 ひろさん、かいとのパパさん、kasamaさん、あすーるさん、【UU】亜依の唄さん、 mimiさん、藤井 拓人さん、きょろ文さん、スマイルさん、高田一輝(姉小路)さん、まーくんさん、bunさん、パリンさん、 Dr.Sさん、長野 美光さん、A.NOUCHIさん、tomhさん、英之さん、16わんさん、みやもーぷんぽさん、そうたさん、tamagonnさん、hiroさん、他 |
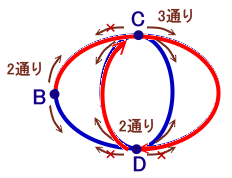
3通りある分岐点に下図のような名前を付けておきます。
出発点Bから進む方向は、上または下の2通り。
次の分岐点(例えば上に進んだ場合C)では、進む方向は4通りありますが、
元の道へは戻れませんから、4−1=3通り。さらに、3番目の分岐点では、進む方向は4通りありますが、
元の道と最終点Bへは進めませんので、4−2=2通り
(上記例では、ここまでの経路はB→C→D→C)。残る経路は一意的に決まるの(上記例では、C→D→B)で、1通り。
従って、
経路数計=2×3×2=12通り
と求まります。答 12通り
以上
解答例2[6*2、経路の並び替え]
| ゴンともさん、太陽の陽さん、ともひろさん、kuri、他 |
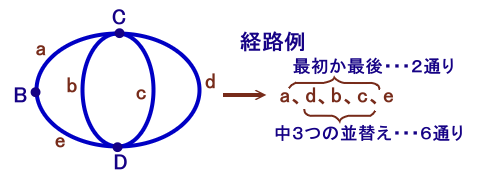
分岐点間をたどる経路は、下図のように5本あります(a、b、c、d、eとします)。
一筆書きの経路は、これら5本を並べ替えることで得られます。
ただし、a、eは、最初か最後にしか並べませんので、2!=2通り、
また、b、c、dは、中3個所のいずれかになるので、3!=6通り。従って、
経路数計=2×6=12通り
と求まります。