問題[平面図形]
|
|
|
|
|
|
|
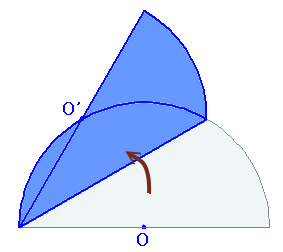 |
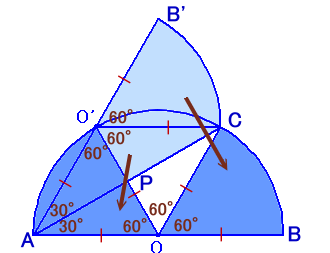
直径が12cmの半円の紙を、 左図のように半円の中心Oが弧の上にくるように折り返しました。 このとき、青色をつけた部分の面積は何cm2ですか? |
|
|
|
|
|
|
解答例1[等積変形で円の3分の1 、等積変形、実は円全体の3分の1、てゆうか円の3分の1系]
| mhayashiさん、N.Nishiさん、kaizerさん、みかんさん、ひろさん、 HAJIさん、阪急大好き!さん、まーくんさん、kasamaさん、 高田一輝(姉小路)さん、あすーるさん、Plutonianさん、ハトさん、Dr.Sさん、 【UU】亜依の唄さん、tamagonnさん、太陽の陽さん、FLONTさん、鉄道アニマルさん、鳳 ナオさん、ふんふんさん、大西将也さん、ボビーさん、他 |
各点に下図のような名前を付けておきます。
OA、OO'、O'Aは、いずれも円の半径なので長さが等しい。
従って、△O'AOは、正三角形、同様に、△O'OCも、正三角形となります。よって、
∠O'AO=∠OO'A=∠O'OA=60°、
∠CO'O=∠O'OC=∠O'CO=60°、
従って、
∠COB=180°−∠O'AO−∠O'OC=60°、
∠B'O'C=180°−∠OO'A−∠CO'O=60°
となります。また、CABを折り返したものがCAB'だから、
∠O'AP=∠PAO=30°よって、扇形B'O'C=扇形B'O'C、△O'PC=△OAPとなります。
従って、
求める面積
=扇形OO'A+扇形OBC
=円の面積×1/6×2
=3.14×6×6÷3=37.68cm2
と求まります。答 37.68cm2
以上
解答例2[重複部分を引く、 図形式]
| ゴンともさん、ハトさん、tomhさん、ふうきさん、おっさん、他 |
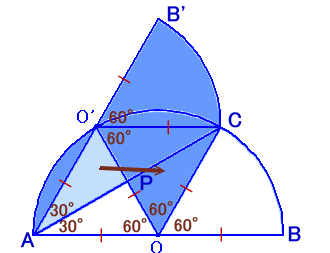
ほぼ解答例1と同様ですが、重複部分を引くことで求めてみます。
元の図形は半円で、重複部分O'AC=弦O'C+△O'AC=弦O'C+△O'OC=円の6分の1
従って、
求める面積=円の2分の1−円の6分の1=円の3分の1=37.68cm2
と求まります。