問題(濃度の問題)
|
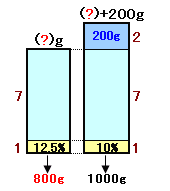
12.5%の食塩水が( ? )gあります。これに水を200g加えると、10%の濃さになります。 |
解答例1[食塩の量を基準に考えた] (ヌオさん、長野美光さん、数楽者さん、他)
食塩の量を1として考えます。
最初の食塩水の濃度は12.5%ですから、食塩水の量は100%/12.5%=8、よって水の量は8-1=7となります。
200gの水で薄めたときの濃度は10%ですから、食塩水の量は100%/10%=10、よって水の量は10-1=9となり、2だけ増加したことになります。
この2が200gに相当するので、元の食塩水の量8は800gに相当することになります。
答:800g
以上
解答例2[食塩の量を基準に(その2)] (Gouさん、 他)
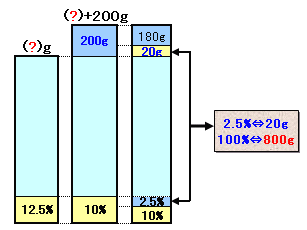
薄めた食塩水を一様に混ぜ合わせ、元の食塩水の量に相当する部分、あとで加えた200gの部分の2つを考えます。
いずれも濃度は10%ですから、200g中の食塩は200g×10%=20gです。
従って、元の食塩水の部分で減少した食塩12.5-10=2.5%に相当する量が20gとなります。
よって、元の食塩水全体100%に相当するのは、20g×100/2.5=800gと分かります。
解答例3[面積図を利用]
(みっちんさん、きょえぴさん、チュパさん、他)
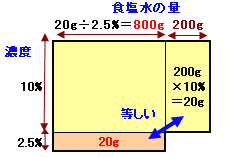
元の食塩水、および薄めた食塩水に含まれる食塩の量を下図のような面積図で表します。
この図では長方形のに濃度、幅に食塩水の量をとりますので、面積=濃度×食塩水の量=食塩の量という関係になります。
2つの長方形の面積(食塩の量)は等しいので、重ねてはみ出た2つの長方形の面積も等しくなります。
薄めた食塩水では、濃度10%、食塩水200gですから、食塩は200g×2%=20gとなります。
従って、元の食塩水の量は20g×100/12.5=800gと分かります。
解答例4[天秤を用いる]
(小杉原啓さん、ふじさきたつみさん、高橋道広さん、POIさん、HALさん、トトロ@Nさん、他)
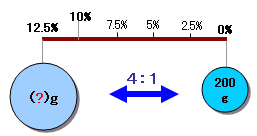
下図のような天秤で考えます。
この天秤では、おもりに2つの食塩水、天秤の長さにそれぞれの濃度に比例した長さを取ります。
この天秤で釣り合う部分の目盛りは、2つの食塩水を混ぜたときの濃度に相当します。
この問題では、天秤の長さの比は(12.5-10):(10-0)=1:4、従っておもりである食塩水は逆比の4:1となります。
よって、元の食塩水は、200g×4=800gとなります。
解答例5[食塩水の薄め方の比を利用] (Taroさん、ヒデー王子さん、 他)
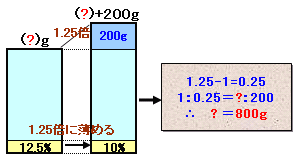
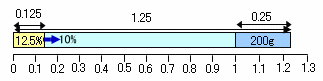
食塩水の濃度は12.5%から10%に減少しますので、1.25倍に薄めたことになります。。
従って、食塩水の量は、1.25-1=0.25だけ増加したことになり、0.25が200gに相当することになります。
よって、元の食塩水は1に相当しますので、200g×1/0.25=800gになります。
解答例6[分数を用いた] (DrKさん、みのちゃん、kakeruさん、他)
濃度を分数で考えます。
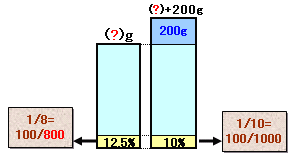
元の食塩水の濃度12.5%は、分数に直すと1/8=100/800、薄めた食塩水の濃度10%は、1/10=100/1000。
2つの分母の差はちょうど200ですから、元の食塩水の量が800gで食塩が100gであったとすると、200gの水で薄めると濃度が10%になり、題意に適します。
解答例7[求める食塩水の量を基準として考える]
(少年さん、ほそたにさん、井﨑大智さん、有無相生さん、他)
元の食塩水の量を1として考えます。
食塩の量は濃度12.5%より0.125、薄めた食塩水の濃度が10%であることから、このときの食塩水の量は0.125×100/10=1.25。
従って、1.25-1=0.25だけ水で薄めたことになり、これが200gであることから、元の食塩水の量は200g×1/0.25=800gとなります。
なお、有無相生さんは薄めたあとの食塩水の量を1として解いています。
解答例8[方程式で解く]
(澪桜葵美翔さん、大希のパパさん、ミミズクはくず耳さん、mhayashiさん、まおさん、他)
考えた方程式は、少しずつ異なりますが、ほぼ共通しています。
m*(0.125-0.1) = 200*0.1 より, m=800
食塩の量=A、食塩水の量=Bとして
A÷B=0.125、A÷(B+200)=0.1最初×12.5÷100=(最初+200)×1
0÷100(1/8)x/(x+200)=1/10
12.5×A=10×(A+200) など
(その他)
- 最初の食塩水を100gに仮定して何グラムの水を加えれば10%になるかを求め、そこから逆算 ・・・ まるケンさん。