第３問の解答

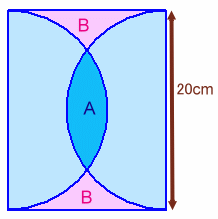
問題（平面図形）

問題図

 左図のように、たての長さが20cmの長方形の中に、半円を2個書き入れました。
このとき、図の青色部分(A)と赤色部分(B)の面積(2か所の合計)が等しくなったとすると、長方形の面積は何cm2あるでしょう？
　

　

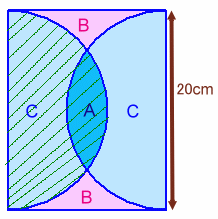
解答例１［半円と半円を重ねて求めた］　
（長野美光さん、辻さん、うっしーさん、澪桜葵美翔さん、大岡敏幸さん、とらいしくるさん、他多数）

半円と半円を重ねてみます。

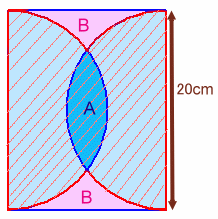
赤色部分(B)以外の面積＝半円の面積×２−青色部分(A)の面積

従って、
　円の面積
＝半円の面積×２
＝赤色部分(B)以外の面積＋青色部分(A)の面積
＝長方形の面積−赤色部分(B)の面積＋青色部分(A)の面積
＝長方形の面積　（赤色部分(B)の面積＝青色部分(A)の面積だから）

よって、
　求める長方形の面積
＝円の面積
＝３．１４×１０2
＝３１４cm2となります。

答：３１４cm2

以上

解答例２［半円の外側部分＝半円］　
　（チュパさん、ミミズクはくず耳さん、とみっちさん、みっちんさん、CRYING DOLPHINさん、パリンさん、N.Nishiさん、他）

１つの半円の面積に着目します。

参考図２

　半円の面積＝C＋A　と表せます。
一方、その外側の面積＝C＋B（２つ分）＝C＋A
従って、半円の面積＝その外側の面積となります。

よって、
　長方形の面積
＝半円の面積＋外側の面積
＝半円の面積＋半円の面積
＝円の面積
＝３１４cm2

(その他)

  • 青の面積を二つに分ける・・・巷の夢さん、ＡＹＵＭＩさん
    （解答例２とほぼ同じ）
    　

  • 正方形を基準にする・・・mitchさん