第４問の解答

問題（和差算？）

 ある商店では、1個が456円の品物Aと654円の品物Bの2種類の商品を販売しています。
ゆたか君は、品物AとBを合わせて11個買う為にちょうどのお金を持ってきたのですが、レジのお姉さんが、Aの値段を654円、Bの値段を456円と勘違いして代金を計算した為に、持っていたお金よりも990円高い代金を請求されてびっくりしてしまいました。
ゆたか君が持ってきたお金はいくらだったのでしょう？

　

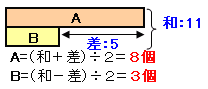
解答例１［和が１１、差が５］　
（井﨑大智さん、パリンさん、BossFさん、Ｅ．Ｔ．さん、きょえぴさん、kunioさん、なにわさん、なかさん、ヒデー王子さん、tekiさん、せなんなさん、あまれっとさん、ちーくん、にゃあさん、とみっちさん、中学への算数学コンさん、山口　勇太郎さん、数楽者さん、ヌオさん、他多数）

参考図１

AとBの価格を取り違えると１個あたりの価格差は654-456=198円 。
合計で990円多くなったことから、AとBの個数の差は990÷198＝5個。

参考図２

個数の和が11、差が5になる組み合わせは、A=8とB=3しかないので、
正しい合計金額は、
　456×8＋654×3＝3648+1972＝5610円
となります。

なお、AB5個ずつの差が990円として解いた、まさきさん、チュパさんの場合も、ほぼこの解答例１と同様です。

答：５６１０円

以上

解答例２［方程式を解く］　

【連立方程式】　（N.Nishiさん、Airさん、巷の夢さん、のざりんさん、どらえもんさん、あくびちゃん、MIKI&RIE&PAPAさん、マジックさん、航介さん、Geniusさん、ＡＹＵＭＩさん、他）

商品Aをx個、商品Bをｙ個買う予定だったとします。
　正しい値段：456x＋654y　・・・（１）
　誤った値段：654x＋456y　・・・（２）

（２）－（１）より、
　198x－198y＝198(x－y)＝990
従って、
　x－y＝5　・・・（３）。

題意より、
　x＋y＝11　・・・（４）
よって、あとは和差算でとけます。

参考図３

（３）＋（４）より、
　2x=11+5、x＝(11＋5)/2＝8
（４）－（３）より、
　2y=11-5、y=(11－5)/2＝3。

よって、正しい値段は、456×8＋654×3＝5610円となります。

［商品Ａの購入個数を未定とした一次方程式を］
　（澪桜葵美翔さん、大岡敏幸さん、みのちゃん、mhayashiさん、他）

Ａをｘ個、Ｂを（１１－ｘ）個買う 予定として一次方程式を作ります。
　正しい金額 = 456ｘ + 654（11－ｘ）
　誤った金額 = 654ｘ + 456（11－ｘ）

正しい金額 + 990 = 誤った金額 より、
　456ｘ + 654（11－ｘ）+ 990 = 654ｘ + 456（11－ｘ）
整理して解くと、 ｘ＝８が得られます。
正しい金額の式に代入して、 456×8 + 654×（11－8） = 5610円となります。

解答例３［正しい値段と間違った値段の和と差］　
　（CRYING DOLPHINさん、うっしーさん、ほわほわさん、他）

参考図４

正しい金額と誤った金額の合計は、品物Ａ、Ｂそれぞれ456円のものと654円のものを１１個ずつ買うことになるので、(456+654)×11=11210円となります。
一方、題意から金額の差は990円なので、和差算により正しい金額は、
　(11210-990)÷2=5610円となります。

なお、品物Ａ 、Ｂを１１個ずつ購入した場合を考えた、まおさん、Noble Scarletさん、nnoさん、東大受験生さんも、解答例３とほぼ同様です。

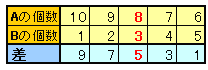
解答例４［あてはめ］　
　（★ぴよぴよ★さん、検非違使さん、トライアングルユウさん、他）

参考図５

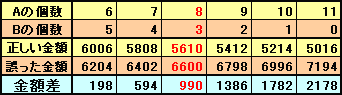
A、Bの個数の和が１１個となるケースを書き出して、正しい金額と誤った金額の差を計算すると上の表のようになります。（金額差がマイナスとなる場合を除く）

従って、題意を満たすのは、A=8個、B=5個の場合で、そのときの正しい金額は５６１０円となります。

解答例５［Aだけ１１個買ったときの前後の差を考えて］　（ねこやんさん、他）

Aだけ１１個買った場合：金額差＝(654-456)×11=2178
Aを１０個、Bを１個の場合：金額差＝(654×10+456×1)-(654×1+456×10)=1782

Aの個数が一個減ると前後の差は、2178-1980=396円ずつ減ります。
従って、差が900円になるには、(2178-990)÷396=3より、
Aを８個、Bを３個買う場合となり、そのときの正しい金額は５６１０円となります。