問題(場合の数)
|
1と書かれたカードが2枚、2と書かれたカードが2枚、3と書かれたカードが2枚あります。 |
解答例1[3×3×3−3]
(まおさん、ふじさきたつみさん、POIさん、小杉原啓さん、高田修成さん、E.T.さん、ペポッチ!さん、トトロ@Nさん、Taroさん、AIRさん、ミミズクはくず耳さん、高橋道広さん、大岡敏幸さん、やまけんさん、中学への算数学コンさん、tekiさん、パリンさん、ヒデー王子さん、なかさん、東大受験生さん、他多数)
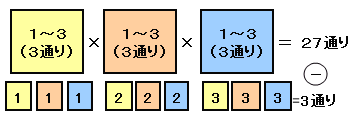
各数字ともカードが3枚あるとしたら、百の位、十の位、一の位とも1〜3の3通り可能となるので、合計では、3×3×3=27通り考えられます。
しかしながら、実際にはカードは2枚ずつしかないので、全ての位の数字が同じである、111、222、333の3通りは題意を満たさない。
従って、求める場合の数は、27−3=24通りとなります。
答:24通り
以上
解答例2[樹形図]
(みっちんさん、あまれっとさん、辻。さん、いまポンさん、ちーくん、みのちゃん、ピカソさん、ヌオさん、ちゅらさん、チュパさん、ゴラさん、NobleScarletさん、マリリンさん、しょうさん、AYUMIさん、makoさん、MIKI&RIE&PAPAさん、他)
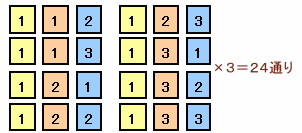
例えば、百の位を1とし、残りの2桁を小さい順に求めると、
112,113,121,122,123,131,132,133の8通りとなります。従って、全部で8×3=24通りとなります。
解答例3[場合分け、全部を列挙、3×6+6、順列を用いた]
(N.Nishiさん、CRYING
DOLPHINさん、きょえぴさん、まるケンさん、東大受験生さん、LIONさん、BossFさん、とみっちさん、巷の夢さん、少年さん、航介さん、数楽者さん、検非違使さん、ねこやんさん、のざりんさん、しょうさん、とらいしくるさん、ktakumiさん、ワタベえさん、nnoさん、DrKさん、他)
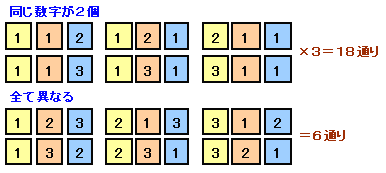
「同じ数字を2個の場合」と「全ての数字が異なる場合」に分けて考えます。
(同じ数字を2個の場合)
例えば1が2枚、2が1枚のとき、112、121、211の3通り。
1が2枚、3が1枚のときも同様に、113、131、311の3通り。
合わせて、1が2枚の場合は、3×2=6通り。2枚同じ数となるのは、1、2、3の3種類考えられるから、
合計、6×3=18通り。(全ての数字が異なる場合)
3個の数字を並べる場合の数(順列)=3×2×1=6通りとなります。
よって、全部で18+6=24通りとなります。