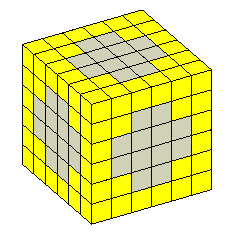
問題(立体図形)
 |
|
解答例1[8×8+2×12]
(小杉原啓さん、ワタベえさん、アユマナさん、E.T.さん、ふじさきたつみさん、ピカソさん、みっちんさん、信三さん、まるケンさん、みのちゃん、やまけんさん、長野美光さん、パリンさん、ゴラさん、なかさん、巷の夢さん、フォルティッシモさん、数楽者さん、大岡敏幸さん、八尾隆史さん、NobleScarletさん、mhayashiさん、ちーくん、BossFさん、香蓮さん、他)
残る小立方体は2種類に分類できます。
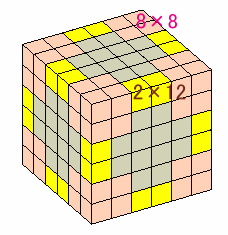
角の2×2×2の立方体が8つで8×8=64個。
辺の1×2の直方体が12個で2×12=24個。
あわせて64+24=88個となります。答:88個
以上
解答例2[上三段数えて2倍]
(ミミズクはくず耳さん、マーチン・ミグスさん、チュパさん、GLKAさん、さんさんさん、マッスルさん、ペポッチ!さん、nnoさん、Taroさん、CRYING
DOLPHINさん、まおさん、辻。さん、いまポンさん、トトロ@Nさん、なにわさん、POIさん、航介さん、tomhさん、きょえぴさん、あくびちゃん、まさきさん、うっしーさん、AIRさん、ヒデー王子さん、ヌオさん、他)
1面ずつスライスして考えます。
対称形だから、1段目から3段目までを考えれば十分です。
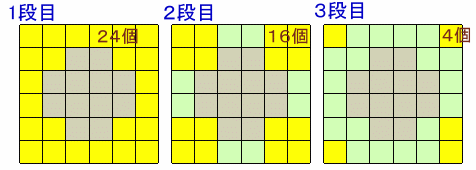
1段目は、見えている通り、抜き取った小立方体が8個、残りは6×6−8=24個。
2段目は、抜き取る小立方体がさらに2×4=8個増えるので、残りは24−8=16個。
3段目は、四隅の4個のみ残ります。
従って、合計では(24+16+4)×2=44×2=88個となります。
解答例3[立方体を8分割して]
(とみっちさん、tekiさん、N.Nishiさん、高橋道広さん、まれっとさん、MIKI&RIE&PAPAさん、康仁さん、他)
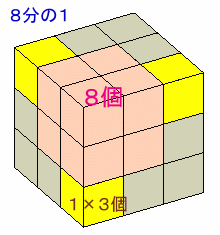
対称形だから立方体の8分の1を考えれば十分です。
2×2×2=8個と1×3=3個で、8+3=11個が残ります。
従って、全体では11×8=88個となります。
解答例4[抜ける立方体は座標でチェック]
(有無相生さん、なかさん、makoさん、すっぴーさん、yatagawaさん、ハラギャーテイさん、他)
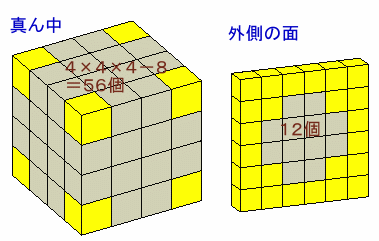
真ん中の4×4×4の立方体と、外側の6つの面に分けて抜き取られる小立方体の数を数えてみます。
真ん中では、隅に1個ずつ小立方体が残るので、抜き取られる小立方体は、4×4×4−8=64−8=56個。
外側の面では、12個×6面=72個。
従って、全体では56+72=128個抜き取られるので、残るのは6×6×6−128=216−128=88個となります。
解答例5[1回づつ切り抜かれた個数を計算した]
(DrKさん、とらいしくるさん、他)
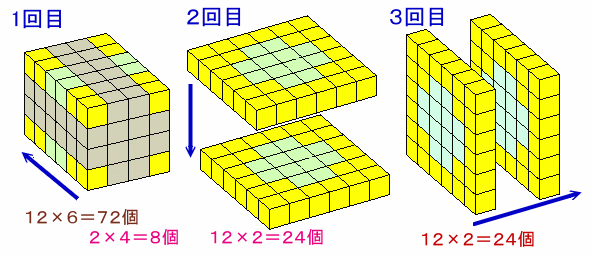
3方向に1回づつ抜き取られる個数を計算していきます。
1回目は、1面当たり十字形の12個を6面抜き取るので、12×6=72個。
2回目は、1面当たり12個を2面の12×2=24個と、真ん中部分の2個×4=8個、計24+8=32個。
3回目は、1面当たり12個を2面の12×2=24個。
従って、全体では72+32+24=128個、
よって残りは6×6×6−126=216−128=88個となります。