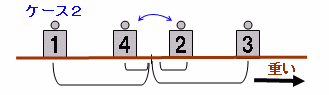
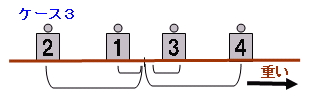
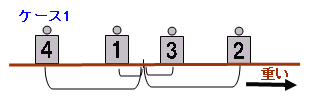問題(その他)
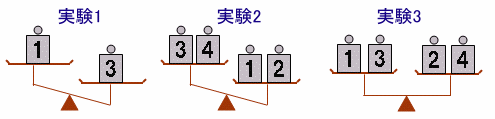
|
上の3つの実験結果から、1番〜4番のおもりを重い順に並べて下さい。 |
解答例1[1+3=2+4の利用]
(巷の夢さん、中学への算数さん、ヒデー王子さん、tekiさん、大岡敏幸さん、有無相生さん、東大受験生さん、tomhさん、チュパさん、MIKI&RIE&PAPAさん、ペポッチ!さん、きょえぴさん、みーちゃんぶちゅうさん、ヒデー王子の弟子4号さん、ななこさん、他)
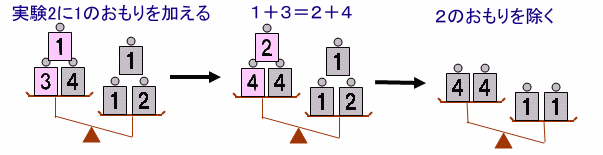
実験2で、両方の天秤皿に1のおもりを加えます。
1+3=2+4なので、左側の1、3のおもりを2、4に変えます。
2のおもりが両方の天秤皿にあるのでこれを除きます。1のおもり2個が4のおもり2個より重いので、1>4が得られます。
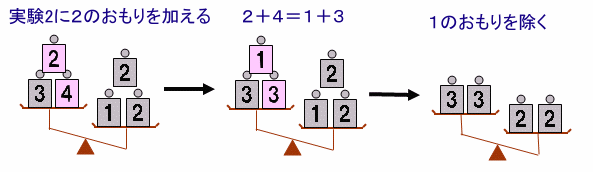
こんどは、実験2で、両方の天秤皿に2のおもりを加えます。
2+4=1+3なので、左側の2、4のおもりを1、3に変えます。
1のおもりが両方の天秤皿にあるのでこれを除きます。2のおもり2個が3のおもり2個より重いので、2>3が得られます。
実験1より3>1が分かっていますから結局、2>3>1>4を得ます。
答:2>3>1>4
以上
解答例2[1と3、2と4の和と差に注目、数直線で考える]
(まるケンさん、ゴラさん、数楽者さん、マッスルさん、まおさん、AIRさん、ふじさきたつみさん、増田弘樹さん、mhayashiさん、みっちん。さん、とみっちさん、のざりんさん、yukiさん、いまポンさん、他)
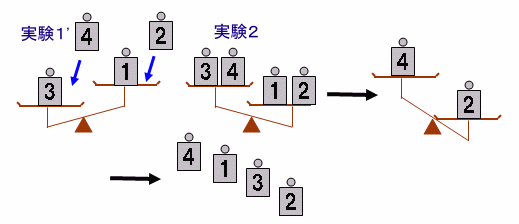
実験1より、3>1となっています。
3の皿に4のおもりを、1の皿に2のおもりを載せると実験2のように、釣り合いが逆転します。
従って、4>2であり、しかも3と1の差より2と4の差のほうが大きくなければなりません。しかも、実験3より1、3の平均と2、4の平均は釣り合っています。
従って、2>3>1>4と分かります。
解答例3[パズル感覚で、まず実験3,1より絞る、平均から考えるなど]
(BossFさん、スギさん、しょうさん、當眞大千さん、ktakumiさん、算数題魔人さん、パリンさん、とらいしくるさん、Taroさん、N.Nishiさん、
ヌオさん、航介さん、nnoさん、あまれっとさん、トトロ@Nさん、POIさん、高橋道広さん、DrKさん、新緑さん、アユマナさん、他)
実験3より、1+3=2+4より、1、3および2、4の平均は一致します。
しかも実験1より3>1となります。そこで、2のおもりと1、3のおもりの大小によって場合分けします。
(1)2>3>1の場合:
1+3=2+4より、2>3>1>4となります。これは、実験2の結果1+2>3+4に合致しますので題意を満たします。
(2)3≧2>1の場合:
1+3=2+4より、3≧4>1となります。
これは、1+2>3+4に反しますので不適。
(3)3>1≧2の場合:
1+3=2+4より、4≧3>1となります。
これは、1+2>3+4に反しますので不適。
以上より、2>3>1>4となります。