問題(整数の性質)
|
100から300までの整数の中で、3で割った余りが2となる奇数は全部で何個あるでしょうか? |
解答例1[3で割ったら2あまる奇数]+1=?、101から301の間の6の倍数の数]
(CRYING
DOLPHINさん、まるケンさん、ゴラさん、みっちん。さん、ターキングさん、マッスルさん、トトロ@Nさん、ふじさきたつみさん、ペポッチ!さん、とらいしくるさん、ごんざえもんさん、とみっちさん、チュパさん、
信三さん、tomhさん、ファイアーさん、かなっちさん、せいみケンケンさん、他)
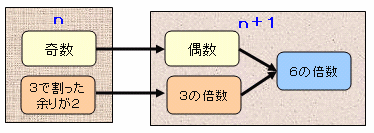
nを3で割ったら2あまる奇数とすると、n+1は偶数かつ3の倍数、すなわち6の倍数となります。
100≦n≦300より、101≦n+1≦301、
この範囲で6の倍数は102〜300で、個数は(302-102)/6+1=34個となります。答:34個
以上
解答例2
[6で割って5余る数はいくつある?、等差数列、数の性質&植木算、(300÷3−100÷3)で奇数が1つ多い、数の性質+和差算]
(小杉原啓さん、ヌオさん、なるさん、有無相生さん、楕淹さん、ツバサさん、E.T.さん、AIRさん、エジソンさん、数楽者さん、ヒデー王子さん、きょえぴさん、東大受験生さん、nnoさん、Taroさん、かっちゃんさん、yasuさん、masaさん、ふうりゅうきさん、 N.Nishiさん、山口勇太郎さん、tekiさん、emikoさん、いまポンさん、ピカソさん、他)
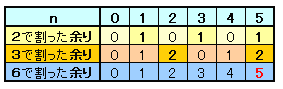
2と3、および最小公倍数の6で割った余りを考えます。
上図より、3で割った余りが2の奇数は、6で割った余りが5の整数となります。
100〜300の範囲で6で割った余りが5の整数は101〜299で、個数は(299-101)/6+1=34個となります。
(その他の解法)
- 1〜200に変換して考えた・・・DrKさん
- 10ずつくぎって法則を調べた・・・大地のパパさん
- 方程式+数えた・・・のざりんさん、やまけんさん、あまれっとさん
- 勘で・・・健人さん、ひろさん、アユマナさん
- EXCELで・・・みのちゃんさん、航介さん
- 全部書く・・・算数題魔人さん
- コンピュータのプログラムで数えた・・・ハラギャーテイさん