問題(整数の性質)
|
15円切手と16円切手だけを使ってちょうど245円にしたいとき、15円切手は何枚使えば良いですか? |
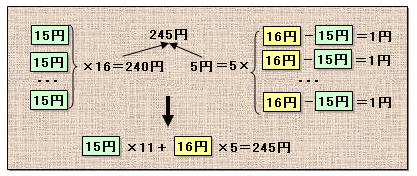
解答例1[16円切手は5枚単位より]
(伝説のマジシャンさん、HAJIさん、有無相生さん、しょうさん、ペポッチ!さん、
ファイアーさん、ヒデー王子さん、とみっちさん、航介さん、tomhさん、みっちん。さん、Takaさん、やまけんさん、
ことぶきさん、星野学園受験生さん、masashiさん、
大岡敏幸さん、MONTANAさん、ぴろりんさん、ma_saさん、他多数)
15円切手が●枚、16円切手が■枚とすると、
15×●+16×■=245 ・・・ (1)
が成り立ちます。(1)より、16×■=245−15×●となり、16円切手の枚数は5の倍数となります。
上表より、16円切手が5枚と15円切手が11枚で、ちょうど245円になります。
答:11枚
以上
解答例2[245より小さい15の倍数から1つずつ増やす]
(ミミズクはくず耳さん、まるケンさん、あまれっとさん、マッスルさん、ピカソさん、POIさん、DrKさん、
パリンさん、アユマナさん、他)
245÷15=16 余り 5、すなわち15×16+5=245より、
15円切手が16枚で240円なので、245円にするには、あと5円分増やす必要があります。15円切手1枚を16円切手1枚と交換すると1円増えるので、5円増やすには5枚交換すればよいことになります。
従って、15円切手が11枚と16円切手が5枚で245円となります。
解答例3[245より大きい16の倍数から1ずつ減らす]
(ヌオさん、ふじさきたつみさん、中村亮さん、tekiさん、BossFさん、他)
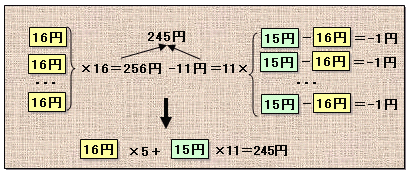
16×15+5=245より、16×16−11=245。
16円切手が16枚で256円なので、245円にするには、11円分減らす必要があります。16円切手1枚を15円切手1枚と交換すると1円減るので、11円分減らすには11枚交換すればよいことになります。
従って、16円切手が5枚と15円切手が11枚で245円となります。
解答例4[245=15×●+16×■の式に変形、245を15で割った余りから、合計枚数を決定し鶴亀算]
(まおさん、naonoriさん、MIKI&RIE&PAPAさん、数楽者さん、nnoさん、とらいしくるさん、c_c_lemon85さん、Taroさん、emikoさん他)
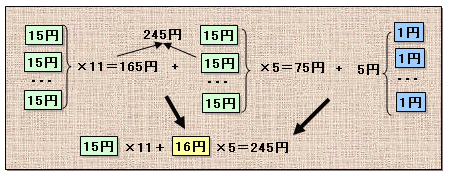
解答例1の(1)式より、
15×●+15×■+■=245
15×(●+■)+■=245 ・・・(2)。解答例2と同様に、
245÷15=16 余り 5、すなわち15×16+5=245。従って、●+■=16、■=5となるようにすればOK。
よって、●=16−■=16−5=11。すなわち、15円切手が11枚と16円切手が5枚で245円となります。
解答例5[15x+16y=245の整数解を順に探索、方程式の自然数解]
(ハラギャーテイさん、小野明日香さん、きょえぴさん、mhayashiさん、他)
解答例3の(2)式より、
15×(●+■)+■=245=15×16+5
15×(●+■−16)=5−■ ・・・(3)従って、5−■は15の倍数となり、5−■=15×▲と表せます。
よって、■=5−15×▲。 ・・・(4)(3)より、●+■−16=▲、
よって、●=▲−(■−16)
=▲−(5−15×▲−16)=11+16×▲。 ・・・(5)(4)、(5)より、●、■が正の整数となるには、▲は0でなければならない。
従って、題意を満たすのは、●=11、■=5のときとなります。
(その他の解法)
全部書き出す。・・・青山学院中等部を目指す人さん、 ツバサさん、かなっちさん
1個だったら、2個だったら、3個だったら・・・って調べて