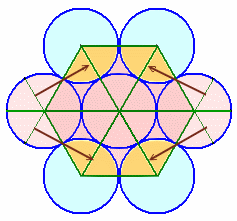
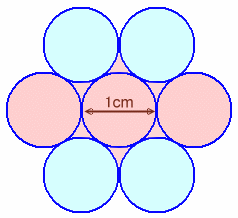
問題(平面図形)
 |
|
解答例1[1辺1cmの正六角形に変形、円の中心を結んだ6角形を作る、円を3個付け足して]
(高橋道広さん、ハラギャーテイさん、数楽者さん、ピカソさん、マッスルさん、小杉原啓さん、nnoさん、ペポッチ!さん、
きょえぴさん、高田壮潔さん、CRYING
DOLPHINさん、有無相生さん、emikoさん、kobaさん、大岡敏幸さん、voidさん、なるさん、BEANさん、検非違使さん、 長野美光さん、ミミズクはくず耳さん、なにわさん、ふじさきたつみさん、みっちん。さん、あまれっとさん、DrKさん、tekiさん、MIKI&RIE&PAPAさん、トトロ@Nさん、航介さん、かなっちさん、mikiさん、yukiさん、まことさん、 N.Nishiさん、他多数)
各円の中心を結ぶと1辺の長さが1cmの正三角形が6個集まった正六角形ができます。
図のように、左右の円から1/3ずつ2個切り取り、上下の円に移動すると、元の図形はちょうど正六角形となります。
従って、求める面積は正三角形の6倍と分かります。
答:6倍
以上
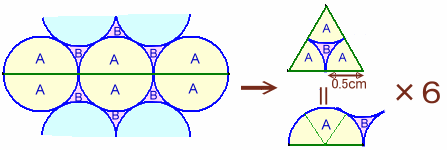
解答例2[正三角形=半円+3つの円に囲まれた部分]
(ヌオさん、とらいしくるさん、AIRさん、まおさん、みのちゃんさん、まるケンさん、haruさん、にっくんさん、他)
互いに接している3つの円の中心を結ぶと1辺が1㎝の正三角形ができるます。
従って、
正三角形の面積
=中心角60度の扇形×3 (A)+3つの円に囲まれた部分 (B)
=円の面積÷2+3つの円に囲まれた部分
となります。求める面積
=円の面積×3+3つの円に囲まれた部分×6
=(円の面積÷2+3つの円に囲まれた部分)×6
=正三角形の面積×6
解答例3[一辺0.5cmの正三角形]
(パリンさん、まこさん、他)
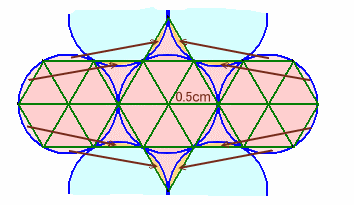
求める図形から8個のレンズ形を移動すると、一辺0.5cmの正三角形24個分と等しくなります。
従って、求める図形の面積は1辺1cmの正三角形の6倍となります。
(その他の解法)
円と円の隙間を出す・・・算数題魔人さん、辻。さん、高田壮潔さん、tomhさん、ともやさん
円と円の隙間の面積を出し(√3/4-π/8)、これを6倍してあとは円(π/4)三つ分足しました。
赤い部分の面積は 3√3/2 となり正三角形の面積 √3/4 の6倍となります。