問題(場合の数)
|
100以下の整数で、2の倍数でも5の倍数でもないものを全て足しあわせると、その合計はいくらになりますか。 |
解答例1[個々に計算、全部の和から2の倍数と5の倍数を引き重複部分を足す]
(マッスルさん、大岡敏幸さん、みっちん。さん、算数題魔人さん、AIRさん、有無相生さん、ミミズクはくず耳さん、ペポッチ!さん、まれっとさん、ふじさきたつみさん、長野美光さん、みのちゃんさん、シマチャンさん、yukiさん、tomhさん、ともやさん、チュパさん、 masashiさん、他多数)
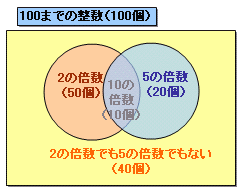
ベン図で考えます。
2の倍数でも5の倍数でもない整数
=(1から100までの整数)−(2の倍数)−(5の倍数)+(10の倍数)
となります。とくに個数は、
・1から100までの整数 ・・・ 100個
・2の倍数 ・・・ 50個(=100÷2)
・5の倍数 ・・・ 20個(=100÷5)
・10の倍数 ・・・ 10個(=100÷10)
より、
・2の倍数でも5の倍数でもない整数 ・・・ 40個(=100-50-20+10)
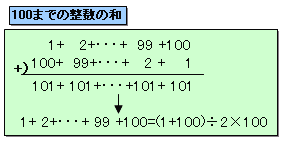
となります。さて、1から100までの整数の和は、上図より、
(1+100)÷2×50=5050
すなわち、等差数列(等間隔に並ぶ数)の和は、
最初の数と最後の数の平均×個数
で計算できます。同様にして、
・2の倍数の和 ・・・ 2550個(=(2+100)÷2×50)
・5の倍数の和 ・・・ 1050個(=(5+100)÷2×20)
・10の倍数の和 ・・・ 550個(=(10+100)÷2×10)
より、
2の倍数でも5の倍数でもない整数の和
=5050−2550−1050+550
=2000個
となります。
答:2000個
以上
解答例2[ガウスの足し算、個数を出して、÷2×100]
(ツバサさん、砂子貴則さん、MIKI&RIE&PAPAさん、ファイアーさん、TORAさん、山口勇太郎さん、C-Dさん、POIさん、TAKOさん、ヒデー王子さん、まるケンさん、航介さん、コンヒキさん、坂梨渓太さん、 takamatsuさん、数楽者さん、他)
整数Nに対して、Nを10で割った商をP、余りをRとすると、
N=P×10+R
と書けます。従って、
Nが2の倍数でも5の倍数でもない≡Rが2の倍数でも5の倍数でもない
こととなりますので、1から10までの整数を調べれば十分です。まず、2の倍数を除くと、
1、3、5、7、9
これから5の倍数を除くと、
Rは
1、3、7、9
となります。よって、求める数は、
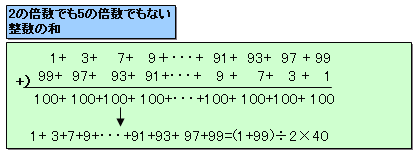
1、3、7、9、 11、13、17、19、・・・、 91、93、97、99
の40個となります。
これらは、等差数列ではありませんが、等差数列と同様に、
(1+99)÷2×40=2000
と計算できます。
解答例3[1の位が1、3、7、9]
(ピカソさん、kobaさん、すっぴーさん、小杉原啓さん、ヌオさん、パリンさん、長野さん、いくぞーさん、あやっちさん、やまけんさん、金子弘平さん、アユマナさん、emikoさん、 他)
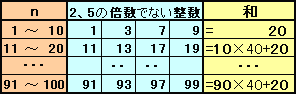
解答例2で分かるように、1の位の数字が1、3、7、9になっている数の合計を求めれば良いことが分かります。
10位の和=(10+20+…+90)×40
=(10+90)÷2×9×40
=50×9×40
=1800
1位の和=(1+3+7+9)×10=200よって、合計は、1800+200=2000個となります。
解答例4[奇数の和−1位が5の和、100×50÷2-5(20×10÷2)]
(きょえぴさん、dr.mさん、N.Nishiさん、ターキングさん、tekiさん、 とらいしくるさん、ごんざえもんさん、他)
解答例2とほぼ同様にして、
2の倍数でも5の倍数でもない整数
=奇数−5の倍数となる奇数
として計算します。奇数の和=1+3+5+・・・+99=(1+99)÷2×50=2500
5の倍数となる奇数=5+15+25+・・・+95
=(5+95)÷2×10=500従って、
2の倍数でも5の倍数でもない整数=2500−500=2000
となります。
(その他の解法)
コンピュータのプログラムを作成・・・まおさん、ハラギャーテイさん、mhayashiさん、
ExcelでMOD関数を使い計算 など