第１６問の解答

問題（場合の数）

問題図

A・B・C・D・E・Fの6人を、3人1組の2組に分けます。
このような分け方は何通りありますか。

解答例１［6Ｃ3 ÷２］　
　（バリケンさん、金子弘平さん、LIONさん、BossFさん、景さん、ktakumiさん、とみっちさん、BEANさん、まるケンさん、信三さん、MIKI&RIE&PAPAさん、山口勇太郎さん、あやっちさん、emikoさん、tomhさん、ちーくんさん、やまけんさん、たかのりさん、ヒデー王子さん、あまれっとさん、tekiさん、ミミズクはくず耳さん、hyuuiさん、ふじさきたつみさん、辻。さん、 他）

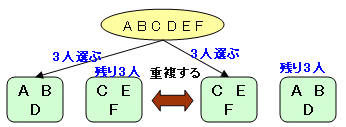
６人から３人を選ぶ組合せは6Ｃ3=２０通り。

参考図１

この組合せは、重複するので実際は、この半分の１０通りとなります。

答：１０通り

以上

解答例２［5人の中から2人を選ぶ］　
（数楽者さん、ファイアーさん、とらいしくるさん、naokiさん、すっぴーさん、yuki:さん、まきおさん、算数題魔人さん、あやっちさん、くもんのけんさん、時枝愛里さん、パリンさん、マッスルさん、ツバサさん、長野美光さん、C-Dさん、ヌオさん、まおさん、きょえぴさん、Taroさん、小杉原啓さん、ＴＯＲＡさん、他多数）

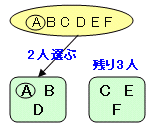
Ａを固定しておいて、Aと同じ組になる２人をB〜Fの５人の中から選ぶことで重複なく求まります。

参考図２

従って、5Ｃ2＝１０ 通りとなります。

（その他の解法）