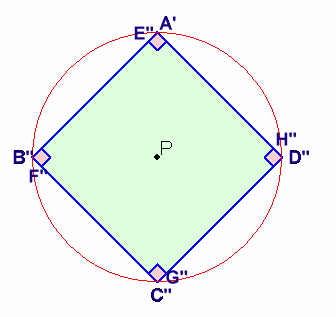
問題(平面図形)
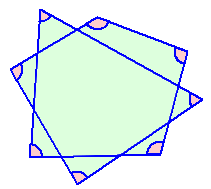 |
|
解答例1[複数の図形に分割し、内角の和の過不足を考える方法]
(1)4角形(360度)x2
(GOMAさん、あまれっとさん、あくびちゃんさん、ぽちさん、N,Fさん、とらいしくるさん、emikoさん、AYUMIさん、ハラギャーテイさん、ハラギャーテイさん、 他)
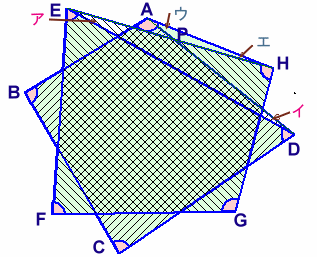
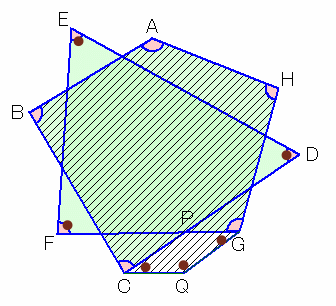
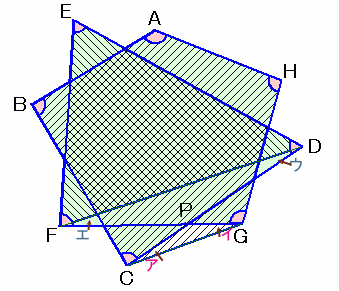
上図のように2つの四角形(四角形ABCD、EFGH)に分けると、内角の和の合計は360×2=720度。
これと求める図形の内角の和を比べると、ア、イの部分を余計に勘定し、ウ、エの部分が計算に入っていない。
四角形ABCD:
∠DAB=∠HAB−∠HAD(ウ)、∠CDA=∠CDE+∠ADE(イ)四角形EFGH:
∠HEF=∠DEF+∠HED(ア)、∠GHE=∠GHA−∠AHE(エ)従って、
(四角形ABCD+四角形EFGH)−求める図形の内角の和
=(ア+イ)−(ウ+エ)ところが、
ア+イ+∠EPD=ウ+エ+∠APH、∠EPD=∠APHより、
ア+イ=ウ+エ
となる。よって、
求める図形の内角の和
=四角形ABCDの内角の和+四角形EFGHの内角の和
=720度
となる。
答:720度
(2)5角形と3角形に分けた
(ねこやんさん、masashiさん、POIさん、渡辺美幸さん、みっちん。さん、N.Nishiさん、ヒデー王子さん、うっしーさん、マッスルさん、DrKさん、 他)
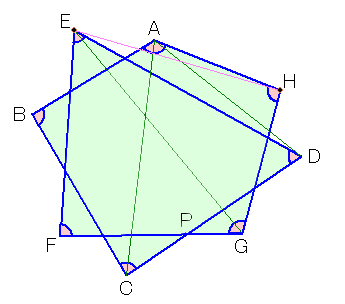
(五角形ABCGH+三角形EFD)−求める図形の内角の和
=(ア+イ)−(ウ+エ)ア+イ=ウ+エより、
求める図形の内角の和
=五角形ABCGHの内角の和+三角形EFDの内角の和
=540度+180度
=720度
(3)三角形を4つにする
(mhayashiさん、天災さん、渡辺美幸さん、麻布さん、ともやさん、ファイアーさん、tub@saさん、まるきくさん、算数題魔人さん、 他)
△ABC+△ACD+△EFG+△EGH
=180度×4=720度△ABC+△ACD=四角形ABDAの内角の和、
△EFG+△EGH=四角形EFGHの内角の和となり、
あとは(1)と同じ。
(4)五角形+四角形-180
(A,NOUCHIさん、大岡 敏幸さん、ターキングさん、BEANさん、tekiさん、きょえぴさん、高田修成さん、他)
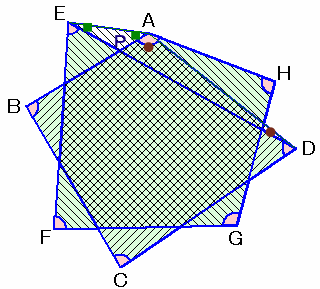
(四角形ABCD+五角形AEFGH)−求める図形の内角の和
=(∠DAB+∠ADE)+(∠AED+∠BAE)
=(∠DAB+∠ADE)+∠APE
=180度(△APDの内角の和)よって、求める図形の内角の和
=(四角形ABCDの内角の和+五角形AEFGHの内角の和)−180度
=360度+540度−180度
=720度
(5)360(四角形の内角和)+180(一直線)×2
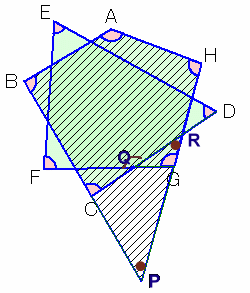
(平野智さん、ごんざえもんさん、C-Dさん、 他)BCおよびHGの延長線が交わる点をPとします。
四角形ABPHの内角の和
=∠A+∠B+∠P+∠H
=∠A+∠B+(∠C−∠R)+∠H四角形EFQDの内角の和
=∠E+∠F+∠Q+∠D
=∠E+∠F+(∠G+∠R)+∠Dよって、
四角形ABPHの内角の和+四角形EFQDの内角の和
=(∠A+∠B+∠C+∠H)+(∠E+∠F+∠G+∠D)
=求める内角の和
=360度×2+360度×2
=720度
(6)最終的には6角形にして (なるさん、辻。さん、他)
FGとCGの交点をP、
Cを通ってFGに平行な直線と、Gを通ってDCに平行な直線の交点をQとします。
∠E+∠F+∠D
=360度−∠FPD
=360度−∠CPG
=∠PCQ+∠Q+∠QGFよって、
求める内角の和
=(∠A+∠B+∠C+∠G+∠H)+(∠E+∠F+∠D)
=∠A+∠B+(∠C+∠PCQ)+∠Q+(∠G+∠QGF)+∠H
=六角形ABCQGHの内角の和
=180度×4
=720度
解答例2[180×8−360×2、内角の和の拡張公式]
(数楽者さん、有無相生さん、カーバンクルさん、みのちゃんさん、トトロ@Nさん、なかさん、TORAさん、 航介さん、算数野郎さん、tomhさん、ふじさきたつみさん、他)
8箇所ある頂点上の(内角+外角)の和
=180×8=1440度うち外角の和
=∠A'AH+∠B'BA+∠C'CB+∠D'DC+∠E'ED+∠F'FE+∠G'GF+∠H'HG
=360×2=720度よって、内角の和=1440−720=720度
解答例3[(180×6+360×1)−360×2、中の7角形に注目]
(タイガさん、小杉原啓さん、QPerさん、すっぴーさん、まおさん、すすき野マンさん、
他)
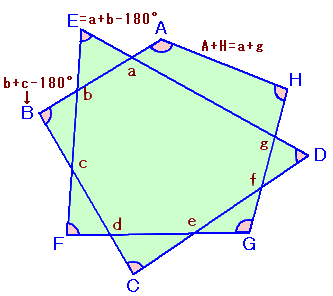
∠DEF=180度−(180度−a)−(180度−b)=a+b−180度 ・・・ (1)
同様に、
∠ABC=b+c−180度 ・・・ (2)
∠EFG=c+d−180度 ・・・ (3)
∠BCD=d+e−180度 ・・・ (4)
∠FGH=e+f−180度 ・・・ (5)
∠CDE=f+g−180度 ・・・ (6)また、 ∠HAB+∠GHA
=360度−(180度−a)−(180度−g)
=a+g ・・・ (7)(1)+(2)+・・・+(7)より、
求める内角の和
=(a+b+・・・+g)×2−180度×6
=180度×5×2−180度×6
=180度×4
=720度
解答例4[(三角形8つ)−2周、普通の8角形−360度] (高橋道広さん、まるケンさん、他)
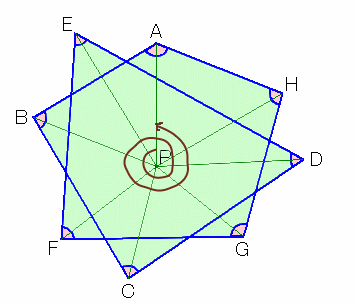
この図形の真ん中に点Pをとり、各頂点とPを結んでできる8つの三角形を考えます。
∠PAB+∠PBA=180度−∠APB
∠PBC+∠PCB=180度−∠BPC
・・・
∠PHA+∠PAH=180度−∠HPAこれらを加えて、
左辺の和=求める内角の和
右辺の和=180度×8−360度×2=720度よって、求める内角の和=720度
解答例5[正八角形埋め込み] (Taroさん、他)
図形の内側の点Pをとり、Pを中心とする円で円周が図形の外側になるものを考えます。
図1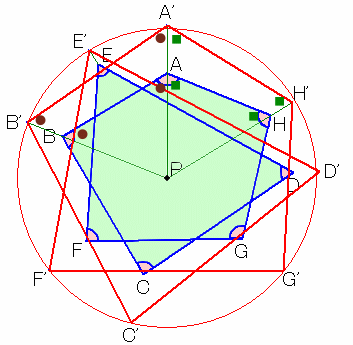 |
図2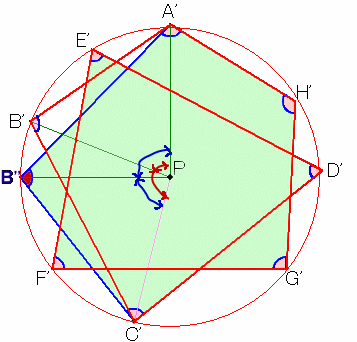 |
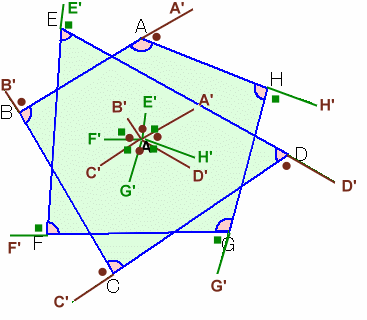
PAの延長線と円の交点をA'、PBの延長線と円の交点をB'、・・・、PHの延長線と円の交点をH'とします。(図1)
∠PAB+∠PBA=∠PA'B'+∠PB'A'=180度−∠APB
同様に、
∠PBC+∠PCB=∠PB'C'+∠PC'B'
・・・
∠PHA+∠PAH=∠PH'A'+∠PA'H'よって、これらを加えると、
∠A+∠B+・・・+∠H=∠A'+∠B'+・・・+∠H'
従って、各頂点が円周上に並んでいる場合でも内角の和は同じになります。次に、A'を固定し、B'が円周上を移動したときを考えます。(図2)
(∠PA'B'+∠PB'A')+(∠PB'C'+∠PC'B')
=(180度−∠A'P'B')+(180度−∠B'P'C')
=360度−∠A'P'C' ・・・ (1)(∠PA'B''+∠PB''A')+(∠PB''C'+∠PC'B'')
=(180度−∠A'P'B'')+(180度−∠B''P'C')
=360度−∠A'P'C' ・・・ (2)(1)、(2)より、
(∠PA'B'+∠PB'A')+(∠PB'C'+∠PC'B')=(∠PA'B''+∠PB''A')+(∠PB''C'+∠PC'B'')よって、各頂点を移動させても内角の和は変わらないことが分かります。
とくに各頂点が等間隔に並んだ場合を考えると(上図)、各頂点の内角は全て90度になります。
従って、内角の和=90度×8=720度となります。(参考)頂点の数がn個で、頂点を結ぶとm周する場合
解答例2、4、5などから、一般的に
内角の和=180度×n−360度×m
と表せます。とくに、n角形については、m=1の場合ですから、
内角の和=180度×n−360度=180度×(n−2)
となります。