第２０問の解答

問題（速さの問題）

A君とB君がマラソンの競走を始めました。ところが走りに自信のあるA君は、油断をしていてB君がスタートしたのに気付かず、ずいぶん出遅れてしまいました。

君が毎分180mの速さで追いかけると10分でB君に追い付き、
毎分240mの速さで追いかけると6分で追いつきます。
では、A君が毎分270mの速さで追いかけたとしたら、何分でB君に追い付きますか？

解答例１［典型的ニュートン算、Bの速度を求めた、相手の進む距離］

　（ペポッチ！さん、バリケンさん、 ヒデー王子さん、haruさん、BEAN さん、増田弘樹さん、コンヒキさん、まこさん、算数野郎さん、ファイアーさん、長野美光さん、小杉原啓さん、じゃまださん、Scaさん、AYUMIさん、あまれっとさん、まるケンさん、まおさん、tub@saさん、C-Dさん、ヌオさん、 カーバンクルさん、平野智さん、 Taroさん、きょえぴさん、 　矢山由紀子さん、GOMAさん、 emikoさん、やまけんさん、 タイガさん、 ヴァンスネックさん、DrKさん、 　辰野さん、他多数）

線分図で考えます。

参考図１

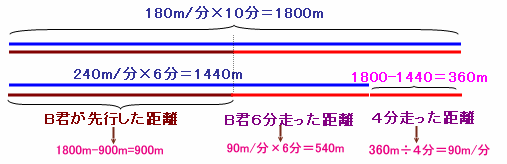
最初、A君は１８０m/分で走り、１０分で追いついたので、
この間１８０m/分×１０分＝１８００m走ったことになります。

今度は、２４０m/分で走り、６分で追いつくので、
この間２４０m/分×６分＝１４４０m走ったことになります。

両者の差＝１８００−１４４０＝３６０mは、B君が一人で走ったことになるので、
B君の速さは、３６０m÷（１０−６）分＝９０m/分となります。

従って、最初A君と一緒に１０分間走った距離は、９０m/分×１０分＝９００m、
よって、B君が先行した距離は１８００−９００＝９００mと分かります。

最後に、A君が２７０m/分で走ると、B君の速さとの差＝２７０−９０＝１８０m/分だけ毎分追いついていくことになるので、９００m÷１８０m/分＝５分で追いつきます。

答：５分

解答例２［AとＢの速さの差の比が５：３］

（受験生その1さん、アントニオ猪木さん、コダック さん、渡辺美幸さん、浜崎あゆみ さん、数楽者さん、マッスル さん、平野智さん、高田修成(修徳学院) さん、トトロ＠Ｎさん、まるきくさん、 他）

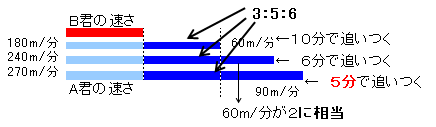
B君が先行した距離を、A君とB君の速さの差で追いついていくので、その比と追いつく時間は逆比例します。

参考図２

従って、最初と２度目でA君とB君の速さの差は、６分：１０分＝３：５となります。
２度目は、最初より２４０−１８０＝６０m/分早いのでこれが５−３＝２に相当します。

３度目は、最初より２７０−１８０＝９０m/分早く走るので、これは３に相当することになり、A君とB君の速さの差は、最初に比べ３：６＝１：２になります。

よって、追いつく時間はこの逆比２：１となるので、１０分×1/2＝５分となります。

解答例３［進行グラフ］ 　（テモさん、とらいしくるさん、みっちん。さん、他）

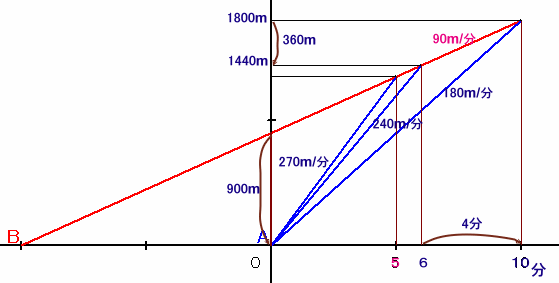
数のようなダイアグラムで考えます。

参考図３

解法としては、解答例１とほぼ同様です。

B君の速さを（１８０×１０−２４０×６）m／（１０−６）分＝９０m/分と求め、
先行距離は１８００m−９０m/分×１０分＝９００mと得ます。
A君が２７０m/分で走るとB君の速さとの差は２７０−９０＝１８０m/分となるので、９００m÷１８０m/分＝５分で追いつきます。

解答例４［面積図］　（算数題魔人さん、ピカソさん、他）

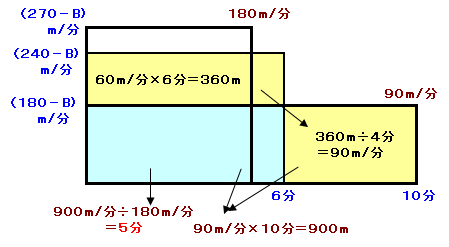
下図のような面積図で考えます。
縦にA君とB君の速さの差、横に走った時間とすると、走った距離をが面積になります。

参考図４

黄色の部分の面積は等しくなります。
左側の黄色の部分は、６０m/分×６分＝３６０mですから、
右側では３６０m÷４分＝９０m/分、これが最初のときのA君とB君の速さの差となります。

従って、B君の先行距離は９０m/分×１０分＝９００m、
３度目は９０＋９０＝１８０m/分で差が縮まるので、９００m÷１８０m/分＝５分で追いつきます。

（その他の解法）