問題(整数の性質)
|
正方形のタイルを図のように規則正しく並べていきます。 100段目まで並べるには、全部で何個のタイルが必要ですか。 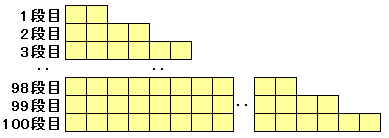 |
解答例1[(1+2+3+......+100)×2、(2+200)×100÷2、2+4+6+・・・・・+200 、(1+100)×100、数列]
(Taroさん、小杉原啓さん、辻。さん、ハラギャーテイさん、みのちゃんさん、 まおさん、shiさん、AIRさん、カーバンクルさん、まッキーさん、 ピカソさん、GOMAさん、マッスルさん、ミミズクはくず耳さん、まるきくさん、 ふじさきたつみさん、かなっちさん、ペポッチ!さん、tekiさん、AYUMIさん、 波ピカさん、BEANさん、ヒデー王子さん、航介さん、やまけんさん、 k,mさん、きょえぴさん、憲坊さん、うっしーさん、
マリー姫さん、受験生その1さん、テモさん、ムーさん、そうさんさん、 emikoさん、ともやさん、masashiさん、まいのぱぱさん、 マスターハンドさん、ああさん、gottiさん、 とらいしくるさん、Ayamiさん、すてさん、yuukoさん、ヨッシーさん、 悠基さん、 ねこやんさん、 絵里ちゃんのパパさん、K.Hさん、mhayashiさん、他多数)等差数列の和の公式を利用します。
初項をa、公差をd、最終項をb、n項までの和をSとすると、
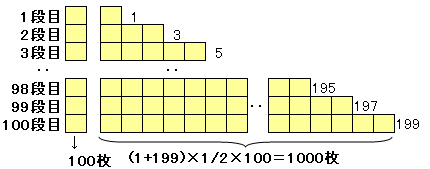
S=(a+b)×n×1/2 ・・・ (1)とくに、a=1、d=1、n=100のとき、b=100となり、
(1+2+3+......+100)=(1+100)×100×1/2=5050本問では、この2倍になるのでの10100枚となります。
あるいは、直接公式(1)を適用して、
S={2+200}×100×1/2
=101×100
=10100枚
となります。答:10100枚
解答例2[100×202÷2]
(ヌオさん、あまれっとさん、有無相生さん、マリー姫さん、コダックさん、 tomhさん、栗原英治さん、nnoさん、タツさん、なかさん、 なかさん、ヴァンスネックさん、ヒアデスさん、他多数)
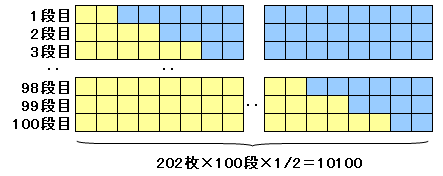
同じ数だけタイルを増やして、上図のように100×202の長方形を作ります。
この長方形のタイルの枚数は、答えの2倍だけあるので、
答えは、100×202÷2=10100枚です。これは、解答例1の公式を次のようにして求めるのと同じです。
公差をdととすると、b=a+(n-1)d。S= a +(a+d)+ ・・・+{a+(n-2)d}+{a+(n-1)d} ・・・ (2)
逆から足して、
S={a+(n-1)d}+{a+(n-2)d}+ ・・・+ (a+d) +a ・・・ (3)よって、(2)+(3)より、
2S={2a+(n-1)d}×n
S=[a+{a+(n-1)d}]×n×1/2
=(a+b)×n×1/2
解答例3[(2+200)×50]
(N.Nishiさん、まるケンさん、算数野郎さん、大岡 敏幸さん、算数題魔人さん、 パリンさん、haruさん、あきらさん、団子3兄弟の息子さん、sanoさん、 他多数)
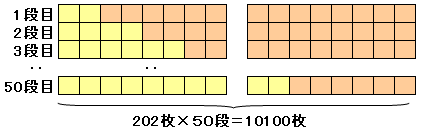
1段目2枚と100段目200枚を足すと202枚
2段目4枚と99段目198枚を足して202枚
3段目6枚と98段目196枚を足して202枚
・・・・
50段目100枚と51段目102枚を足して202枚
従って、、202枚が50組できるので、総数は、202×50=10100枚
解答例4[100×100+100、(100×200)/2+100]
(TORAさん、トトロ@Nさん、西原大輔さん、 ピ9ティさん、他多数)
左端の縦1列を別に数えます。
n番目までの合計は、この1列だけでn個。
他の部分は、1+3+5+・・・+(2n-1)=n×n個。 ←奇数の和:(1)で、a=1、d=2、b=2n-1
よって、合計はn×n+nと表わされる。とくに、100番目までなら、100×100+100=10100個