第２３問の解答

問題（平面図形）

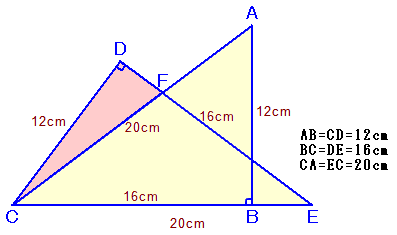
図のように、∠B＝∠D＝90度の合同な直角三角形を重ねて書きました。
赤色の部分の面積は何cm2ありますか。

問題図

　

解答例１［FCEが二等辺三角形からFEを求める］

（まるケンさん、mhayashiさん、小杉原啓さん、トトロ＠Ｎさん、 カーバンクルさん、コダックさん、まおさん、有無相生さん、信三さん、 ヌオさん、マッスルさん、とらいしくるさん、GOMAさん、ふじさきたつみさん、算数さん、BEANさん、AIRさん、パリンさん、tomhさん、 AYUMIさん、toshiさん、emikoさん、ヒデー王子さん、POIさん、きょえぴさん、kobaさん、まいのぱぱさん、他多数）

参考図１

△FCEは、底角が等しいから二等辺三角形。
FからCEに下ろした垂線の足をGとすれば、
△FCGと△FEGは合同で元の△ACBと相似。

これらの三角形は３辺の比が3：4：5。
GE＝20÷2＝10cmだから、FE＝(10)×(5/4)＝12.5cm。
よってDF＝16−12.5＝3.5cm

求める△DCFの面積は、12×3.5÷2＝21cm2

答：２１cm2

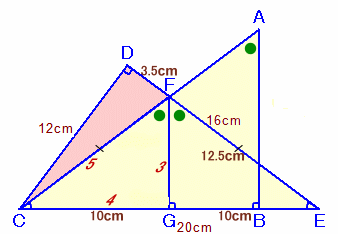
解答例２［FCEが二等辺三角形だけど・・・、ＦＣＥを半分にして高さを求める］

（N.Nishiさん、あまれっとさん、BONZさん、算数題魔人さん、ムーさん、 ミミズクはくず耳さん、ピカソさん、
算数題魔人さん、まるきくさん、ヨッシーさん、ふくしんさん、他多数）

前半部分は解答例１と同じ。
FG＝10×3/4cm。

　△DCF
＝△CED−△FBE
＝16×12÷2−20×10×3/4÷2
＝96−75
＝21cm2

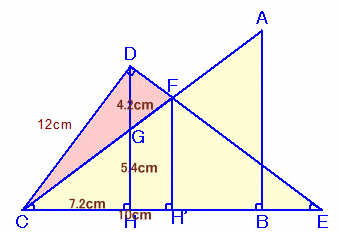
解答例３［DからCEに垂線]

　（Taroさん、tekiさん、ねこやんさん、他 ）

参考図２

DからCEに垂線DHを引き、CFとの交点をGとする。また、Fから垂線FH'を引く。
△CDH、△GCHはともに△ACBと相似で、３辺の比は3：4：5。

よって、
　CH＝CD×３÷５＝１２×３÷５＝７．２cm
　DH＝CD×４÷５＝１２×４÷５＝９．６cm
　GH＝CH×３÷４＝７．２×３÷４＝５．４cm
　DG＝DH−GH＝９．６−５．４＝４．２ｃｍ

△FCEは２等辺三角形だから、
　CH'＝CE÷２＝２０÷２＝１０ｃｍ

従って、
　△DCF
＝△DCG＋△DGF
＝DG×CH'÷２
＝４．２×１０÷２
＝２１ｃｍ2

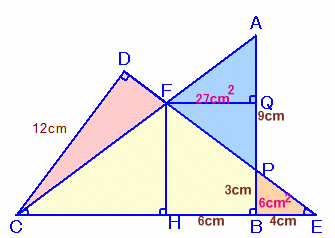
解答例４［はみ出した部分の面積は等しい、相似の関係を使った]

　（大地のパパさん、受験生その1さん、mitchさん、DrKさん、他 ）

DEとABの交点をPとし、FからCEとABにおろした垂線の足をHおよびQとする。

参考図３

△ACBと△DCEは合同だから、お互いの三角形のはみ出した部分の面積は等しい。
よって、△DCG＝△AFP−△PEB　・・・　（１）

△ＰＥＢは△ＡCBと相似で、３辺の比が３：４：５より、
　ＢＥ＝CE−CB＝２０−１６＝４ｃｍ、
　ＢＰ＝BE×３÷４＝４×３÷４＝３ｃｍ
よって、△PEB＝４×３÷２＝６ｃｍ2　・・・　（２）

FQ＝CB−CH＝１６−１０＝６ｃｍ、
AP＝AB−PB＝１２−３＝９ｃｍ、
よって、△AFP＝９×６÷２＝２７ｃｍ2　・・・　（３）

（１）、（２）、（３）より、△DCG＝２７−６＝２１ｃｍ2

（その他の解法）