第２４問の解答

問題（確からしさ）

A、B、Cの3人でじゃんけんを行なうと、手の出し方は全部で27通りあります。

このうち「あいこ」になるパターンが9通りあるので、「あいこになる確率」は、9/27を約分した1/3と言えます。

では、「Aが勝つ確率」はどれだけになりますか？それ以上約分できない分数で答えなさい。

解答例１［A勝ちが何通りあるか調べた］

（ＴＯＲＡさん、ねこやんさん、きょえぴさん、みのちゃんさん、コダックさん、 iinoueさん、DrKさん、有無相生さん、C-Dさん、パリンさん、 辻。さん、ヨッシーさん、マッスルさん、tomhさん、Ayamiさん、 ヌオさん、FF0.5さん、yasuさん、まるきくさん、トトロ＠Ｎさん、 ミミズクはくず耳さん、電波の傀儡さん、BEANさん、kobaさん、大岡　敏幸さん、 ピカソさん、団子3兄弟の息子さん、ムーさん、SNOOPYさん、ふじさきたつみさん、 すっぴーさん、shiさん、ちょみやさん、NobleScarletさん、TAKOさん、 nikonikoさん、長野美光さん、masashiさん、ktakumiさん、 石田さきさん、石田さきさん、他多数）

参考図１

２７通りの手の出し方を、Aが勝ち、負け、引き分けの３パターンで分類してみると、上図のようにそれぞれ９通りあるので、Aが勝つ確率は９/２７＝１/３となります。

なお、２７通り全てを調べなくても、Aがグー、チョキ、パーを出す確率は同じであり、また対象性から、出す手がいづれの場合もAが勝つ確率は等しいので、例えばパーを出すときの９通りだけを調べる方法でも充分です。
この場合は、９通りのうち、勝ち、負け、引き分けとも３通りずつなので、勝つ確率は３/９＝１/３。

答：１/３

解答例２

n人でじゃんけんをする場合に一般化します。
Ａがパーを出す場合を考えます。（チョキ、グーでも全く同様）

Ａが勝つためには、残りの(n-1)人ともパーか、グーのどちらかを出さなくてはなりません。もし、誰か一人でもチョキを出す人がいれば、Ａは負けるか引き分けになるからです。

従って、この確率は、(2/3)n-1になります。

ただし、全ての人がパーを出した場合は引き分けになるので、この確率(1/3)n-1を除く必要があります。

よって、Ａが勝つ確率は、(2/3)n-1−(1/3)n-1となります。

同様に、Ａが負ける確率も、(2/3)n-1−(1/3)n-1となります。
従って、引き分けの確率は、１−｛(2/3)n-1−(1/3)n-1｝×２となります。

特に、n=3のとき、
Ａが勝つ確率、および負ける確率は、
　(2/3)2−(1/3)2＝4/9-1/9＝3/9＝1/3
引き分けの確率は、１−1/3×２＝1/3となります。

（その他の解法）　いずれも誤り

参考図２

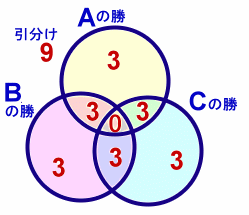
実際、上図のように、２７通りある手の出し方のうち、たまたまＡ、Ｂ、Ｃが勝つ場合がそれぞれ９通りになっているので、勝つ確率が1/3になっているのです。

このことが成り立つのは、解答例２で分かるように、n=2、3のときだけです。