第２５問の解答

問題（平面図形）

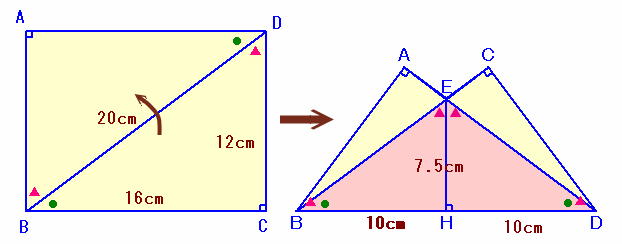
たて12cm、横16cmの長方形の紙を、対角線を折り目にして折り返します。
このとき紙が重ならない部分の面積は、合わせて何cm2になりますか？

解答例１［重なった部分の2倍を引く］

（小杉原　啓さん、まおさん、ねこやんさん、あまれっとさん、コダックさん、 トトロ＠Ｎさん、あきらさん、長野美光さん、まるケンさん、AIRさん、 tekiさん、BONZさん、AYUMIさん、kobaさん、GOMAさん、 高田壮潔さん、BEANさん、ムーさん、nikonikoさん、AROHAさん、 ニコロビンさん、他多数）

元の長方形をABCDとします。

参考図１

対角線BDで分割した２つの直角三角形BDA、DBCは縦１２cm、横１６cmより、辺の長さの比が３：４：５の直角三角形となります。
よって、BD＝BC×５/４＝２０cm。

長方形ABCDを対角線BDで折り返したときADとBDの交わる点をEとし、
EからBDに下ろした垂線の足をHとします。

すると、△EBHと△EDHは合同で、△DBCと相似になります。

よって、BH=HD=BD×1/2＝１０cm、EH＝BH×３/４＝７．５cm。

従って、△EBD＝BD×EH×1/2＝２０×７．５×1/2＝７５cm2。

よって、重ならない部分の面積
　＝長方形ABCD−△EBD×２
　＝１６×１２−７５×２
　＝４２cm2。

答：４２cm2

解答例２［3:4:5から対角線を20cmと判断して］

（ＴＯＲＡさん、きょえぴさん、有無相生さん、ヌオさん、ピカソさん、 パリンさん、ミミズクはくず耳さん、N.Nishiさん、DrKさん、 tomhさん、なにわっこフジさん、ふじさきたつみさん、masashiさん、AROHAさん、 福田英成さん、平野智さん、他多数）

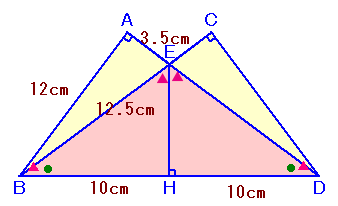
下図は、解答例１と同じ。

参考図２

EB＝ED＝BH×５/４＝１２．５cm。
AE＝EC＝BC−BE＝１６−１２．５＝３．５cm。

従って、△ABE＝△CDE＝３．５×１２×1/2＝２１cm2。

よって、重ならない部分の面積＝△ABE＋△CDE＝４２cm2。

解答例３［三平方の定理使いました、方程式、重ならない三角形の直角と交わっている長さ］

（辻。さん、takuさん、まこさん、ヨッシーさん、カーバンクルさん、 大岡　敏幸さん、とらいしくるさん、Taroさん、せっきいさん、ぶる〜は〜ちゅさん、mkuraさん、他 ）

参考図３

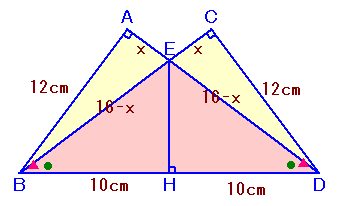
△ABEと△CDEは合同な直角三角形です。
AE=CE=xとすると、EB＝ED＝16-xとなります。

三平方の定理より、
　x2＋１２2＝(１６-x)2
　x2＋１４４＝２５６-３２x＋x2
　３２x＝１１２
よって、x＝３．５cm。

以下、解答例２と同じ。

解答例４［三角関数を用いる］

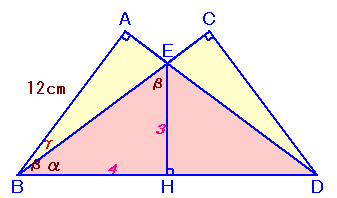
∠DBC＝α、∠BDC＝β、∠ABE＝γとします。

参考図４

tanα＝3/4、tanβ＝4/3となります。
γ＝β−αより、三角関数の加法定理を用いると、
tanγ＝（tanβ−tanα）／（１＋tanβ・tanα）
　　　＝（4/3-3/4）/(1+4/3・3/4)
　　　＝7/24。

従って、AE＝AB・tanγ＝１２×7/24＝３．５cm。
以下、解答例２と同様。

（その他の解法）