問題(推理)
|
a、b、c、d4人のグループがあります。
では、4人の中で本当のことを言っているのは誰々でしょう? |
解答例1[本当のことを言う人数で場合分け]
(C-Dさん、つる太さん、ふじさきたつみさん、有無相生さん、まるケンさん、 GOMAさん、tekiさん、tomhさん、とらいしくるさん、まおさん、AIRさん、トトロ@Nさん、ミミズクはくず耳さん、Taroさん、 信三さん、あきらさん、長野 美光さん、数楽者さん、ぶる〜は〜ちゅさん、 やまけんさん、りおさん、mhayashiさん、他多数)
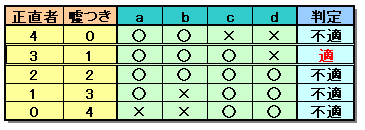
本当のことを言う人数で場合分けして表にします。
それぞれのケースで、各人の言っていることが正しければ○、嘘であれば×をつけると、
正直者が3人のケースのみが適します。このとき、正しいことを言っているのは、a、b、cの3人です。
以上
答 a、b、c
解答例2[aとcから決める]
(辻。さん、あまれっとさん、コダックさん、ハヤさん、BossFさん、 三木さん、きょえぴさん、ギップルさん、あさみゆうたさん、takuさん、 チュパさん、ゆーさん、ゆーさん、他 )
『正直者が0人』とすると全員嘘つきなので、cが言っている「嘘つきが1人以上いる」も嘘になり矛盾します。
『嘘つきが0人』とすると全員正直者なので、cが言っている「嘘つきが1人以上いる」も正しくなり矛盾します。
従って、正直者も嘘つきも1人以上いることが分かります。
よって、a、cは正しいと言うことになります。すると、正直者が2人以上いることになるので、bも正しいことを言っています。
これから、残るdが嘘を言っていることになります。結論として、a、b、cの3人が正しいことを言い、dが嘘を言っていることになります。
これは題意に適します。
解答例3[aから順に]
(小杉原 啓さん、Ayamiさん、ねこやんさん、マスターハンドさん、パリンさん、 arakiさん、マッスルさん、ヨッシーさん、りんごさん、桔梗屋さん、 ヌオさん、算数題魔人さん、他 )
まず、「正直者が1人以上いる」と言うaが嘘だと全員が嘘つきとなり、「嘘つきが1人以上いる」というcも嘘となり全員が正直者となるので 矛盾。
よって、aは正しい。次に、「正直者が2人以上いる」と言うbを嘘とすると、正直者は1人以下で嘘つきが3人以上となりますが、このとき「嘘つきが1人(または2人)以上いる」というc、dも正しいこということになり矛盾。
故にbも本当。次に、「嘘つきが1人以上いる」というcを嘘とすると、嘘つきが1人もいないことになり、c自身 の発言と矛盾。
よって、cも本当。最後に、dを本当とすると、前の3人が本当と分かっているので全員が正直者となり、d自身の発言と矛盾。
よって、dは嘘。以上から、a、b、cが本当で、dが嘘と分かります。これらは各人の発言と矛盾がでない ので題意に適します。
(その他の解法)
- dを基準に場合分け:
TORAさん、BEANさん、たくみさん、masashiさん、
- 嘘のことを言う人数で場合分け
NobleScarletさん、すてさん、
(参考)拡張問題
|
a1〜an、b1〜bnの2n人のグループがあります。(ただし、nは偶数) それぞれが、グループ内の人の発言について話しています。
では、この中で本当のことを言っているのは誰々でしょう? |
解答例2と同様にして、「正直者が0人」、「嘘つきが0人」はどちらも矛盾となりますので、
まずa1、b1の2人は正しいことが分かります。すると、「正直者が2人以上」とするa2も正しくなり、合わせて3人が正しくなります。
よって、「正直者が3人以上」とするa3も正しくなり、合わせて4人が正しくなります。
以下同様にして、a1〜anの全員が正しいことが分かります。さて、kを1≦k≦nとして、bkが正しいとします。
bkは「k人以上嘘つき」と言っているので、それより少ない人数以上が嘘つきというb1〜bk-1も正しいことになります。このようなkの最大値をmとします。(1≦m≦n)
もし、m=nとすると、全員正しくなり、「嘘つきがいる」と言うb1〜bnの発言と矛盾しますので、m<n。よって、b1〜bmのm人が正しく、bm+1〜bnの(n-m)人が嘘となります。
従って、m≦n-mで、かつm+1>n-mでなければなりません。
これから、n/2-1/2<m≦n/2となり、nが偶数であることから、n/2は整数、
よって、m=n/2となります。以上から、本当のことを言っているのは、
a1〜an、およびb1〜bm(ただし、m=n/2)
となります。ちなみに、n=2のとき、本問題の場合と一致します。
以上