第２９問の解答

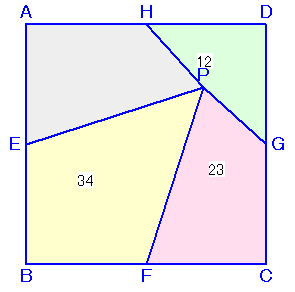
問題（平面図形）

問題図
左図で、ABCDは正方形、E、F、G、Hは各辺の中点です。

正方形内部の点Pで正方形を4つの四角形に分けたときの面積が 、
３カ所については、12cm2、23cm2、34cm2と分かっています。

では、残りの1カ所の面積は何cm2ありますか。

　

解答例１［12＋34−23＝23、三角形の面積］

（ＴＯＲＡさん、トトロ＠Ｎさん、mhayashiさん、あまれっとさん、ヒノ茶さん、 AIRさん、ヌオさん、長野美光さん、mkuraさん、まるケンさん、 emikoさん、ミミズクはくず耳さん、LIONさん、有無相生さん、算数題魔人さん、 QPerさん、小杉原　啓さん、kunioさん、tekiさん、糸貫算数さん、 tomhさん、数楽者さん、たかパパさん、NobleScarletさん、 ヒデー王子さん、本ちゃんさん、maruhagedonさん、きょえぴさん、masashiさん、 あきらさん、ちょみやさん、　天才ユウリンさん、他多数）

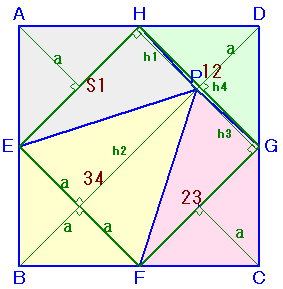
E、F、G、Hを結んでできる正方形EFGH（１辺の長さの半分をａとおきます）の面積は、正方形ABCDのちょうど半分になります。
ここで、△PHE、△PEF、△PFG、△PGHの高さをh1、h2、h3、h4とします。

参考図１

　四角形PHAE＝△PHE＋△HAE＝1/2×2a（a＋h1）　・・・　（１）
　四角形PＥＢＦ＝△PＥＦ＋△ＥＢＦ＝1/2×2a（a＋h2）　・・・　（２）
　四角形PＦＣＧ＝△PＦＧ＋△ＦＣＧ＝1/2×2a（a＋h3）　・・・　（３）
　四角形PＧＤＨ＝△PＧＨ＋△ＧＤＨ＝1/2×2a（a＋h4）　・・・　（４）

(1)+(3)より、
　四角形PHAE＋四角形PＦＣＧ＝a（2a＋h1＋h3）

(2)+(4)より、
　四角形PＥＢＦ＋四角形PＧＤＨ＝a（2a＋h2＋h4）

h1+h3=h2+h4=2aが成り立つので、
　四角形PHAE＋四角形PＦＣＧ＝四角形PＥＢＦ＋四角形PＧＤＨ＝４ａ2
＝正方形EFGH

よって、
　四角形PHAE＋２３＝３４＋１２
　四角形PHAE＝３４＋２４−２３＝２３ｃｍ2

以上

答　２３ｃｍ2

解答例２［面積の等しい部分を記号で］

（ねこやんさん、N.Nishiさん、つる太さん、ふじさきたつみさん、わにがわさん、 パリンさん、ブースカさん、グリフィンドールさん、やまけんさん、A.NOUCHIさん、 娘。さん、たくみさん、ごまちゃんさん、他 ）

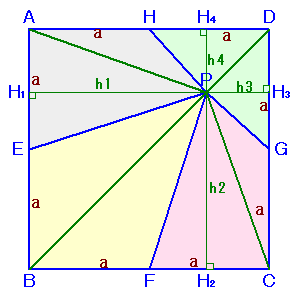
正方形ＡＢＣＤの１辺の長さの半分をａとします。
また、ＰからＡＢ、ＢＣ、ＣＤ、ＤＡへ下ろした垂線の足をH1、H2、H3、H4とします。

参考図２

ＰＨ1＝h1、ＰＨ2＝h2、ＰＨ3＝h3、ＰＨ4＝h4とおくと、
　四角形PHAE＝△PHＡ＋△ＰAE＝1/2×a（h1＋h2）　・・・　（１）
　四角形PＥＢＦ＝△PＥＢ＋△ＰＢＦ＝1/2×a（h2＋h3）　・・・　（２）
　四角形PＦＣＧ＝△PＦＣ＋△ＰＣＧ＝1/2×a（h3＋h4）　・・・　（３）
　四角形PＧＤＨ＝△PＧＤ＋△ＰＤＨ＝1/2×a（h4＋h1）　・・・　（４）

(1)+(3)より、
　四角形PHAE＋四角形PＦＣＧ＝1/2×a（h1＋h2＋h3＋h4）＝２ａ2

(2)+(4)より、
　四角形PＥＢＦ＋四角形PＧＤＨ＝1/2×a（h1＋h2＋h3＋h4）＝２ａ2

よって、
　四角形PHAE＋四角形PＦＣＧ＝四角形PＥＢＦ＋四角形PＧＤＨ

従って、
　四角形PHAE＋２３＝３４＋１２
　四角形PHAE＝３４＋２４−２３＝２３ｃｍ2