問題(場合の数)
|
|
|
|
|
|
|
 |
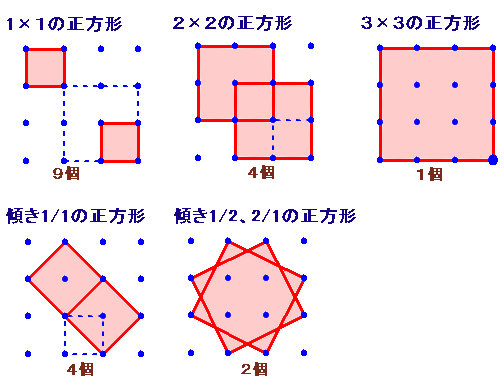
左図のように、16個の点が碁盤目状にならんでいます。 この点の中の4点を結んで正方形を作るとき、4つの点の選び方は何通りありますか。 |
|
|
|
|
|
|
解答例1[直立(9+4+1)とななめ(4+2)、5種類数え上げ]
| ミミズクはくず耳さん、信三さん、コダックさん、ふじさきたつみさん、C-Dさん、
SNOOPYさん、トトロ@Nさん、あまれっとさん、マッスルさん、
tomhさん、つる太さん、nikonikoさん、ハヤさん、ねこやんさん、
コンチ4XXXXさん、ちょみやさん、masashiさん、きょえぴさん、パリンさん、
tekiさん、きよたんさん、A.NOUCHIさん、三木さん、りんごさん、
TOMOKIさん、ほなみさん、かんきちさん、takamatsuさん、ヒデー王子さん、
ギップルさん、104さん、mhayashiさん、
高田修成(修徳学院)さん、みのちゃんさん、ヌオさん、有無相生さん、あきらさん、 GOMAさん、大岡 敏幸さん、長野美光さん、数楽者さん、カーバンクルさん、 emikoさん、BEANさん、ウッキー・タクヤさん、ウリさん、やまけんさん、 根本雄大さん、まおさん、算数題魔人さん、とらいしくるさん、kobaさん、 あさみゆうたさん、ryo sagawaさん、他 |
直立のものと斜めのものに分けて数えます。
(直立のもの)
辺の長さが1cm ・・・ 右隅の頂点が来る位置で考えると、3×3=9個
辺の長さが2cm ・・・ 〃 、2×2=4個
辺の長さが3cm ・・・ 〃 、1×1=1個
計=9+4+1=14個
(斜めのもの)
傾きが1/1のもの ・・・ 右隅の頂点が来る位置で考えると、2×2=4個
傾きが1/2、2/1のもの ・・・ 2個
計=4+1=6個
よって、合計14+6=20個となります。
答 20個
以上
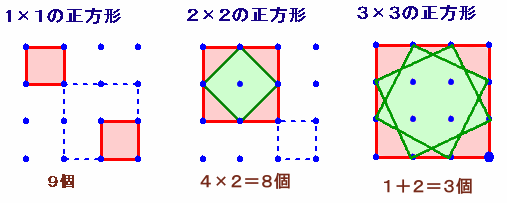
解答例2[(1×9)+(2×4)+(3×1)]
| TORAさん、Taroさん、まるケンさん、AIRさん、きょえぴさん、 きょえぴさん、ステップ ばい ステップ (たかパパ)さん、他 |
直立する正方形は解答例1と同じ。
傾いた正方形を、直立する正方形に内接するものを考えると、
2×2の正方形に ・・・ 各1個×4=4個
3×3の正方形に ・・・ 2個
と求まりますので、合計=1×9+4×2+3×1=20個となります。
(その他の解法)
・点をパターン分けし、その点を使った正方形 ・・・ わにがわさん、
碁盤の目のようにある16の点を、角の点4個・・A、辺にある点8個・・B、内部にある点4個・・Cとし、
Aを通る正方形3パターン×4個、Bを通る正方形5パターン×8個、Cを通る正方形7パターン×4より80個を得ます。ただし、この数え方は、正方形の各頂点を選んだときに1個ずつ数えるので4倍に重複して数えていることになりますから、80÷4=20個が求める個数となります。