問題(平面図形)
|
|
|||
|
|
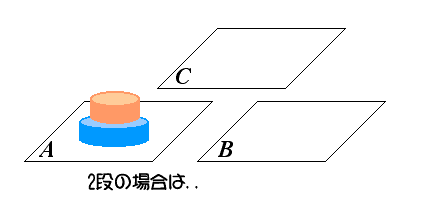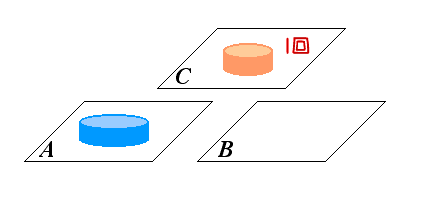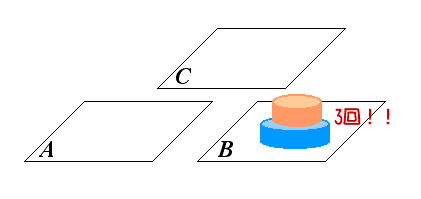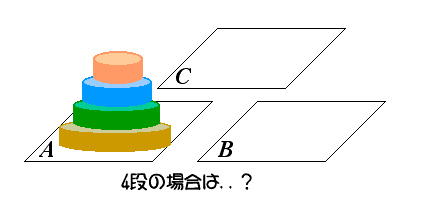 |
ハノイの塔という遊びがあります。 これは大きい順に積み重ねられたブロックをAのテーブルからBのテーブルに1個ずつ移動させるもので、この際にCのテーブルも含めた3つのテーブルを使うことができます。 ただし移動の際に、小さいブロックの上に、それよりも大きいブロックを重ねることはできません。 ブロックが2個の場合は、左図のように3回の操作で移動が完了します。 ではブロックが4個の場合、少なくとも何回の操作が必要ですか |
|
|
|
|
||
解答例1[7+1+7、ブロック2個・3個の場合を利用]
| TORAさん、ふじさきたつみさん、トトロ@Nさん、きっちょむさん、仮面Xさん、
半田 彬倫さん、maruhagedonさん、 C-Dさん、千鶴。さん、あまれっとさん、ちょみやさん、しまねこさん、 松本 時博さん、他 |
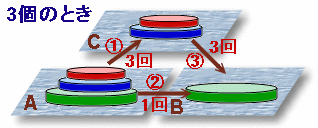
(3個のとき)
上の2個をCへ移動 ・・・ 3回
下の1個をBへ移動 ・・・ 1回
上の2個をCからBへ移動 ・・・ 3回
合計:3+1+3=7回
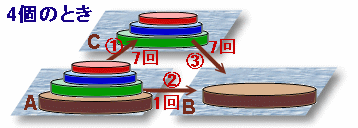
(4個のとき)
上の3個をCへ移動 ・・・ 7回
下の1個をBへ移動 ・・・ 1回
上の3個をCからBへ移動 ・・・ 7回
合計:7+1+7=15回 となります。
答 15回
以上
解答例2[2^4-1]
| Banyanyanさん、Taroさん、小杉原 啓さん、辻。さん、tekiさん、 ミミズクはくず耳さん、GOMAさん、きょえぴさん、やまけんさん、AIRさん、 tomhさん、鈴木さん、mkuraさん、大岡 敏幸さん、クララさん、 ヒデー王子さん、テモさん、他 |
一般化して、ブロックがn個のときの移動回数をAnとします。
解答例1と同様に考えると、
An=2An-1+1 ・・・ (1)
が成り立ちます。(1)を変形して、
An+1=2(An-1+1)=・・・=2n-1(A1+1)=2n-1(1+1)=2nよって、An=2n−1 となります。
とくに、A4=24−1=16−1=15回となります。
(その他の解法)
- ブロックの積み上げ ・・・
GROMITさん、有無相生さん、あさみゆうたさん、 三木さん、マスターハンドさん、チュパさん、とらいしくるさん、ほなみさん、 A.NOUCHIさん、GROMITさん、他- 頭の中で動かした。 ・・・
ヌオさん、長野美光さん、コダックさん、パリンさん、修平さん、 わにがわさん、yuukoさん、西 信好さん、算数題魔人さん、きよたんさん、 道家 尚秀さん、ヴァンスネックさん、スモークマンさん、ねこやんさん、nnoさん、 kobaさん、青二才さん、takamatsuさん、桜井太郎さん、mhayashiさん、 他